Работа № 5

Обработка очередей

Цель работы: приобрести навыки работы с типом данных «очередь», представленным в виде одномерного массива и односвязного линейного списка, провести сравнительный анализ реализации алгоритмов включения и исключения элементов из очереди при использовании указанных структур данных, оценить эффективности программы по времени и по используемому объему памяти.

Краткие теоретические сведения

Очередь – это последовательный список переменной длины, включение элементов в который идет с одной стороны (с «хвоста»), а исключение – с другой стороны (с «головы»). Принцип работы очереди: первым пришел – первым вышел, т. е. First In – First Out (FIFO).

Для «хвоста» и «головы» очереди используют соответственно два указателя Pin и Pout,. то есть, исключается элемент с адресом Pout и включается элемент по адресу Pin. Моделировать простейшую линейную очередь можно как на основе вектора (одномерного массива), так и на основе динамического списка.

Реализация очереди в виде массива. При моделировании простейшей линейной очереди на основе одномерного массива выделяется последовательная область памяти из m мест по L байт, где L – размер поля данных для одного элемента размещаемого типа. В каждый текущий момент времени выделенная память может быть вся свободна, занята частично или занята полностью.

В начале процесса очередь пуста, при этом: Pin = Pout =Q1, где Q1 – адрес (индекс) первого элемента очереди, а количество элементов очереди (K) равно нулю. При включении очередного элемента в очередь он располагается по адресу Pin, а сам указатель Pin перемещается на длину типа данных к началу следующего элемента (рис. 1). На рисунке символом Х обозначена память, занятая элементами очереди, при этом считаем, что под массив была выделена область памяти от Q1 до Qm.

            Q1   Q2                                                 Qm

 


                                                                                                

                                                                                         

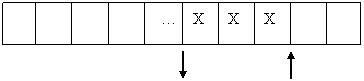                                Pout                              Pin    

Рис. 1

В очереди исключается элемент, находящийся по адресу (индексу) Pout, а указатель Pout, как и в случае добавления, перемещается к следующему элементу. Переполнение очереди наступает, когда указатель «хвоста» Pin перейдет границу последнего элемента, т. е. возникает ситуация, при которой Pin = Qm+L. Причем, переполнение наступает независимо от состояния Pout, т. е. когда, несмотря на наличие свободной памяти слева от Pout нет возможности поместить следующий элемент. Чтобы не случалось переполнения, при каждом исключении из очереди обычно производят сдвиг всех элементов к «голове». Тогда переполнение произойдет лишь  в том случае, если все m мест выделенной памяти заняты. Но на эти последовательные сдвиги затрачивается время. Поэтому более эффективно использовать кольцевую очередь. (рис. 2). Добавление происходит в первые ячейки массива, если «хвост» массива занят.

                     Q1    Q2                                                         Qm   

 

Х       Х                                          Х     Х       Х

 
 

                              Pin                                 Pout 

Рис. 2

При равенстве Pin = Qm+L, означающем, что «хвост» вышел за конец очереди, производят коррекцию: Pin = Q1. Если Pout > Q1, то еще имеется свободное место. В случае кольцевой очереди может быть Pin > Pout, (т. е. «хвост» располагается дальше от начала массива, чем «голова») и Pin < Pout, (т. е. «хвост» ближе к началу массива, чем  «голова»). При равенстве Pin = Pout, означающем, что «хвост» и «голова» совпали, очередь может быть как пустой, так и заполненной (т. е. K=0  или K=m).

В кольцевой структуре нет необходимости сдвигать элементы, но зато сложнее реализовать алгоритмы включения и исключения элементов. Но даже в этом случае проблема переполнения радикально все равно не решается, так как при заполнении очереди возможна ситуация, когда следующий элемент будет «затирать» первый, что потребует дополнительных проверок заполнения очереди. Граничные адреса очереди являются параметрами физической структуры. Эта структура обычно дополняется дескриптором очереди, в котором хранятся имя очереди, адреса нижней и верхней границ очереди, адреса включения и исключения элементов (Pin и Pout), а также максимальное количество заполненных элементов и описание (тип)  элемента очереди.

Реализация очереди в виде линейного списка. Большинство проблем, возникающих при реализации очереди в виде массива, устраняется при реализации очереди на основе односвязного линейного списка, каждый элемент которого содержит информационное поле и поле с указателем «вперед» (на следующий элемент). В этом случае в статической памяти можно либо хранить адрес начала и конца очереди, либо – адрес начала очереди и количество элементов. Исходное состояние очереди: Pout = Pin –  пустой указатель, K = 0.

Основные операции над очередью: включение элемента в очередь и исключение элемента из очереди.

Как было сказано выше, включение элемента в очередь осуществляется по адресу Pin, указатель «вперед» у включаемого элемента – пустой. В этом случае размер очереди ограничивается только объемом доступной памяти. Исключается элемент, находящийся по адресу Pout. Указатель Pout при этом переместится на предыдущий элемент. При исключении элемента необходимо следить за опустошением очереди, а также не забывать освобождать память под удаляемый элемент.

При физической реализации очереди в виде односвязного линейного списка дескриптор будет отличаться отсутствием верхней границы очереди. В этом случае объем очереди ограничивается только объемом доступной оперативной памяти.

В процессе моделирования очереди может оказаться, что при последовательных запросах на выделение и освобождении памяти под очередной элемент выделяется не та память, которая была только что освобождена при удалении элемента. Участки свободной и занятой памяти могут чередоваться, т.е. может возникнуть фрагментация памяти.

Задание

Система массового обслуживания состоит из обслуживающих аппаратов (ОА) и очередей заявок двух типов, различающихся временем прихода и обработки. Заявки поступают в очереди по случайному закону с различными интервалами времени (в зависимости от варианта задания), равномерно распределенными от начального значения (иногда от нуля) до максимального количества единиц времени. В ОА заявки поступают из «головы» очереди по одной и обслуживаются за указанные в задании времена, распределенные равновероятно от минимального до максимального значений (все времена – вещественного типа).

Требуется смоделировать процесс обслуживания первых 1000 заявок первого типа, выдавая после обслуживания каждых 100 заявок первого типа информацию о текущей и средней длине каждой очереди и о среднем времени пребывания заявок каждого типа в очереди. В конце процесса необходимо выдать на экран общее время моделирования, время простоя ОА, количество вошедших в систему и вышедших из нее заявок первого и второго типов.

Очередь необходимо представить в виде вектора и списка. Все операции должны быть оформлены подпрограммами. Алгоритм для реализации задачи один, независимо от формы представления очереди. Необходимо сравнить эффективность различного представления очереди по времени выполнения программы и по требуемой памяти. При реализации очереди списком нужно проследить, каким образом происходит выделение и освобождение участков памяти, для чего по запросу пользователя необходимо выдать на экран адреса памяти, содержащие элементы очереди при добавлении или удалении очередного элемента.

Длительности обработки заявок и интервалы между их приходом (единицы времени – е.в.) – случайные равномерно распределенные числа вещественного типа в указанном диапазоне (например, от t1 до t2). Для получения случайной величины в указанном диапазоне значений можно использовать генератор случайных чисел с параметром функции от 0 до 1, возвращающий значение t. Используя линейное преобразование time = (t2–t1)*t + t1 можно получить необходимое время. Имея время прихода первой заявки, допустим, tприхода1= time, можно определить время прихода следующей заявки как tприхода2 = tприхода1+ time. Следовательно, время прихода 1000 заявок будет равно

tприхода= 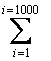tприходаi

Среднее время прихода или обработки заявок можно подсчитать как среднее арифметическое временного диапазона (например, если t1 = 1, а t2 = 4, то среднее время будет равно tср = (1+4)/2 = 2.5). Аналогичным образом рассчитывается время окончания обработки заявок и время выхода заявок из системы.

В один и тот же момент времени одна заявка может придти в очередь, а другая – начать обрабатываться или выйти из системы. Допустим, пришла заявка первого типа, а в этот же момент заявка второго типа закончила обработку и вышла из системы, т.е. tприхода1 = tобработки2  =  tвыхода2.  Таким образом, модельное время прихода заявки первого типа в систему и модельное время выхода заявки второго типа из системы совпали. Процессы обработки одной заявки и прихода другой заявки идут одновременно, т.е. протекают во времени параллельно, а не последовательно.

В приложении приведены примерные варианты заданий.

Указания к выполнению работы

Рассогласование между средними ожидаемыми временами и временами, полученными в моделирующей программе должно быть не больше 1–2%.

При проверке работы программы по входу заявок ожидаемое время моделирования равно среднему интервалу между приходом заявок, умноженному на количество вошедших заявок. Если есть две очереди, то проверка ведется по каждой из очередей.

При проверке работы программы по выходу заявок ожидаемое время обработки в ОА должно быть равно среднему времени обработки заявки, умноженному на количество обработанных заявок. Если есть две очереди и один аппарат, то это будет сумма времен обслуживаний заявок каждого типа.

Если среднее время обработки заявок больше среднего интервала между их поступлением, то очередь будет расти и время моделирования будет определяться временем обработки заявок. При этом количество вошедших заявок должно быть равно времени моделирования, деленному на средний интервал между приходом заявок.

Если средний интервал между поступлением заявок больше или равен среднему времени их обработки, то длина очереди стабилизируется (может стремиться к нулю, единице или к какой-то другой величине) и время моделирования будет определяться временем прихода заявок. При этом ОА может работать с простоем, если время окончания обработки заявки будет меньше, чем время прихода очередной заявки. Тогда время простоя будет определяться разницей этих времен, т. е. tпростоя = tобработки –- tприхода.  Общее время простоя ОА будет равно сумме простоя перед обслуживанием каждой заявки, если простой имел место.

Если есть одна очередь и два аппарата, соединенных последовательно, то время моделирования будет определяться временем обработки в наиболее загруженном аппарате.

Необходимо привести тестирование программы. Рассмотрим пример.

Программа представляет собой модель очереди. Никакие данные в программу не вводятся.

В течение всего времени работы в очередь поступают заявки по случайному закону с временами в интервале от 0 до 10 е. в., обслуживаются заявки по случайному закону со временами в интервале от 0 до 2 е. в.

Каждая заявка после обслуживания в аппарате возвращается в «хвост» очереди для повторной обработки и после 4-х циклов обслуживания покидает систему.

После выхода из системы обработки каждой 100-й заявки выводится текущее состояние очереди, а именно количество вошедших и вышедших заявок, текущая длина очереди и среднее время пребывание заявок в очереди.

Система завершает свою работу по выходу из нее 1000 заявок. На экране при этом отображается общее время моделирования, время простоя ОА, количество вошедших и вышедших из очереди заявок.

После окончания работы следует проверить правильность результатов моделирования.

Теоретически рассчитываем время моделирования. Время обработки заявки лежит в интервале от 0 до 2 е.в., значит среднее значение времени обработки одной заявки 1 е.в. Так как каждая заявка обрабатывается 4 раза до выхода из системы, то среднее время обработки одной заявки будет: 1*4=4 е.в., а общее время обработки 1000 заявок будет: 1000*4 = 4000 е.в. Для прихода 1000 заявок, если каждая приходит в среднем за 5 е.в. потребуется 5000 е.в. Следовательно, ОА работает с простоем и время моделирования будет определяться временем прихода заявок, т.е. оно должно быть равно 5000 е.в. Время простоя будет равно разнице между временем обработки заявок и временем их обслуживания: 5000 – 4000 = 1000 е.в.

На практике при выполнении программы получены следующие  результаты:

время моделирования  –  5054.458 е.в.

время простоя  составило – 987.971 е.в.

вошедших заявок было  –  1018

вышедших заявок – 1000

аппарат сработал – 4019 раз

время работы ОА составило   t = 1*4019 = 4019 е.в.

Сравниваем практические результаты с теоретическими расчетами.

Для проверки правильности работы системы по входу общее время моделирования делим на время прихода одной заявки:

5054.458 / 5 = 1010.8 заявок ~ 1011 заявок

Определяем предполагаемое количество вошедших заявок, фактически их пришло 1018, т.е. погрешность составляет

|100%(1018-1011)/1011| = 0.692%

Проверим правильность работы системы по выходу. За время моделирования аппарат работал 4019 е.в. и простаивал – 987.971 е.в. Время моделирования должно было составить: 5006.971 е.в., а оно составило – 5054.458. Получаем погрешность:

100%(5054.458–5006.971)/5006.971 = 0.9484%.

Вычислим погрешность еще по-другому. Расчетное время работы равно 5000е.в., а фактическое –  5054.458,тогда погрешность составит

100%(5054.458-5000)/5000 = 1,08916%.

Таким образом, проверка работы системы по входным и выходным данным показала, что погрешность работы системы составляет не более 1.1%, что удовлетворяет поставленному условию.

Интерфейс программы должен быть понятен неподготовленному пользователю. При разработке интерфейса программы следует предусмотреть:

·        возможность изменения времен прихода и обработки заявок с экрана;

·        наличие пояснений при выводе результата;

·        вывод процента погрешности работы программы.

Кроме того, нужно вывести на экран время выполнения программы при реализации очереди списком и массивом, а также требуемый при этом объем памяти.

При тестировании программы необходимо:

o       проверить правильность работы программы при различном заполнении очередей, т.е., когда время моделирования определяется временем обработки заявок и когда определяется временем прихода заявок;

o       отследить переполнение очереди, если очередь в программе ограничена.

При реализации очереди списком необходимо тщательно следить за освобождением памяти при удалении элемента из очереди. При этом по запросу пользователя должны выдаваться на экран адреса памяти, содержащие элементы очереди при добавлении или удалении элемента очереди. Следует проверять, происходит ли при этом фрагментация памяти (выделение непоследовательных адресов память).

Содержание отчета

Отчет по лабораторной работе должен содержать выводы, о том, в каких случаях применение какой структуры данных более целесообразно для реализации очереди, какую выгоду дает та или иная реализация. Выводы должны быть подтверждены результатами числовых сравнений расходования памяти и времени выполнения схожих операций.

В отчете по лабораторной работе также должны быть даны ответы на следующие вопросы:

1.Что такое очередь?

2.Каким образом и какой объем памяти выделяется под хранение очереди при различной ее реализации?

3.Каким образом освобождается память при удалении элемента из очереди при ее различной реализации?

4.Что происходит с элементами очереди при ее просмотре?

5.Каким образом эффективнее реализовывать очередь. От чего это зависит?

6.В каком случае лучше реализовать очередь посредством указателей, а в каком – массивом?

7.Каковы достоинства и недостатки различных реализаций очереди в зависимости от выполняемых  над ней операций?

8.Что такое фрагментация памяти?

9.На что необходимо обратить внимание при тестировании программы?

10.  Каким образом физически выделяется и освобождается память при динамических запросах?

Отчет должен быть представлен в электронном или печатном виде.

Список рекомендуемой литературы

  1. Вирт Н. Алгоритмы и структуры данных: Пер. с англ. СПб.: Невский диалект, 2001. С. 69–71, 205–235.

2.       Ахо А.,. Хопкрофт Д., Ульман Д.  Структуры данных и алгоритмы.: Пер. с англ.  М.: Издат. дом «Вильямс», 2000.  С. 58–61.

3.       Кормен Т., Лейзерсон Ч., Ривест Р., Алгоритмы: построение и анализ: Пер. с англ. М.: МЦНМО, 2001. С. 194 –198.

 

Приложение

Примерные варианты заданий

1. Система массового обслуживания состоит из обслуживающего аппарата (ОА) и очереди заявок двух типов (рис. 3).

           T1                                           T2,Т3

 

                                            T3

 

Рис. 3

Заявки первого типа поступают в "хвост" очереди по случайному закону с интервалом времени Т1, равномерно распределенным от 0 до 5 единиц времени  (е.в.). В ОА они поступают из "головы" очереди по одной и обслуживаются также равновероятно за время Т2 от 0 до 4 е.в., после чего покидают систему.

Единственная заявка второго типа постоянно обращается в системе, обслуживаясь в  ОА равновероятно за время Т3 от  0 до 4 е.в. и  возвращаясь в очередь не далее  4-й позиции от "головы". В начале процесса заявка второго типа входит в ОА, оставляя пустую очередь. (все времена – вещественного типа)

Требуется смоделировать процесс обслуживания первой партии из 1000 заявок первого типа, выдавая после обслуживания каждых 100 заявок первого типа  информацию о текущей и средней длине очереди, количестве вошедших и вышедших заявок и среднем времени пребывания заявок в очереди, а в конце процесса – общее время моделирования, время простоя аппарата, количество вошедших в систему и вышедших из нее заявок первого типа и количество обращений заявок второго типа. Обеспечить по требованию пользователя выдачу на экран адресов элементов очереди при удалении и добавлении элементов. Проследить, возникает ли при этом фрагментация памяти.

 

2. Система массового обслуживания состоит из двух обслуживающих аппаратов (ОА1 и ОА2) и двух очередей заявок. Всего в системе обращается 100 заявок (рис. 4).

                                       Т1               1-Р                           Т2

 

 

 


                                                       Р

Рис. 4

Заявки поступают в "хвост" каждой очереди; в ОА заявки поступают из "головы" очереди по одной и обслуживаются по случайному закону за интервалы времени Т1 и Т2, равномерно распределенные от 0 до 6 и от 1 до 8 единиц времени (е.в.) соответственно. (все времена – вещественного типа)  Каждая заявка после ОА1 с вероятностью Р=0.7 вновь поступает в "хвост" первой очереди, совершая новый цикл обслуживания, а с вероятностью 1–Р входит во вторую очередь. В начале процесса все заявки находятся в первой очереди.

Требуется смоделировать процесс обслуживания до выхода из ОА2 первых обслуженных первой партии из 1000 заявок, выдавая после обслуживания в ОА2 каждых 100 заявок информацию о текущей и средней длине каждой очереди, количестве вошедших и вышедших заявок и среднем времени пребывания заявок в очереди, а в конце процесса – общее время моделирования, время простоя аппаратов, количество заявок, прошедших через ОА1.

По требованию пользователя выдавать на экран адреса элементов очереди при удалении и добавлении элементов. Проследить, возникает ли при этом фрагментация памяти.

 

3.      Система массового обслуживания состоит из обслуживающего аппарата (ОА)и очереди заявок (рис 5).

 

   T1                                                    T2           1-Р

 

                                           Р

 

Рис. 5

Заявки  поступают в "хвост" очереди по случайному закону с интервалом времени Т1, равномерно распределенным от 0 до 6 единиц времени (е.в.). В ОА заявки поступают из "головы" очереди по одной и обслуживаются также равновероятно за время Т2 от 0 до 1 е.в., Каждая заявка после ОА с вероятностью Р=0.8  вновь поступает в "хвост" очереди, совершая новый цикл обслуживания, а с вероятностью 1–Р покидает систему. (все времена – вещественного типа) В начале процесса в системе заявок нет.

Требуется смоделировать процесс обслуживания первой партии из 1000 заявок, выдавая после обслуживания каждых 100 заявок  информацию о текущей и средней длине очереди, количестве вошедших и вышедших заявок и среднем времени пребывания заявки в очереди, а в конце процесса – общее время моделирования, время простоя аппарата, количество срабатываний аппарата. По требованию пользователя выдать на экран адреса элементов очереди при удалении и добавлении элементов. Проследить, возникает ли при этом фрагментация памяти.

 

4. Система массового обслуживания состоит из обслуживающего аппарата (ОА) и двух очередей заявок двух типов (рис. 6).

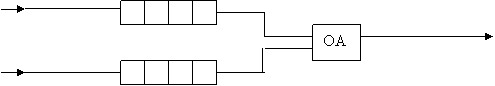   T1                                                                    T3          

 

   Т2                                                                                                                

 

                                                                          Т4                  

Рис. 6

Заявки первого и второго типов поступают в "хвосты" своих очередей по случайному закону с интервалами времени Т1 и Т2, равномерно распределенными от 1 до 5  и от 0 до 3 единиц времени (е.в.) соответственно. В ОА заявки поступают из "головы" очереди по одной и обслуживаются также равновероятно за времена Т3 и Т4, распределенные от 0 до 4 е.в. и от 0 до 1 е.в. соответственно, после чего покидают систему. (все времена – вещественного типа)  В начале процесса в системе заявок нет.

Заявка второго типа может войти в ОА, если в системе нет заявок первого типа. Если в момент обслуживания заявки второго типа в пустую очередь входит заявка первого типа, то она ждет первого освобождения ОА и далее поступает на обслуживание (система с относительным приоритетом ).

Требуется смоделировать процесс обслуживания первой партии из 1000 заявок первого типа, выдавая после обслуживания каждых 100 заявок первого типа  информацию о текущей и средней длине каждой очереди, количестве вошедших и вышедших заявок и среднем времени пребывания заявок в очереди, а в конце процесса – общее время моделирования, время простоя аппарата, количество вошедших в систему и вышедших из нее заявок первого типа и количество обращений заявок второго типа. По требованию пользователя выдать на экран адреса элементов очереди при удалении и добавлении элементов. Проследить, возникает ли при этом фрагментация памяти.