Этап № 6
Обработка разреженных матриц
Цель работы – реализовать алгоритмы обработки разреженных матриц, сравнить эти алгоритмы со стандартными алгоритмами обработки матриц.
Краткие теоретические сведения
В виде матриц достаточно широко представляется информация во многих областях
человеческой жизнедеятельности. Матричные задачи часто используются при решении
разреженных линейных алгебраических уравнений; разреженных обычных и обобщенных
спектральных задач, при этом матрицы могут быть достаточно большие (больше 10![]() элементов), а число
ненулевых элементов при матрице порядка n может выражаться как n
элементов), а число
ненулевых элементов при матрице порядка n может выражаться как n![]() , где g < 1.
, где g < 1.
В подобных матричных задачах значения g лежат в интервале 0.2 … 0.5, т.е. матрица разрежена. Но разреженность матрицы следует учитывать только в том случае, когда из этого можно извлечь выгоду за счет игнорирования нулевых элементов. На самом деле разреженную матрицу можно обрабатывать так же как плотную, и наоборот, плотную матрицу можно обрабатывать так же как разреженную. В обоих случаях получаются правильные числовые результаты, но вычислительные затраты в том или другом случае могут существенно различаться.
Алгоритмы обработки разреженных матриц предусматривают действия только с ненулевыми элементами и, таким образом, количество операций будет пропорционально количеству ненулевых элементов.
Существуют различные методы хранения элементов матрицы в памяти.
Например, линейный связный список, т.е. последовательность ячеек, связанных в определенном порядке. Каждая ячейка списка содержит элемент списка и указатель на положение следующей ячейки. Можно хранить матрицу, используя кольцевой связный список, двунаправленные стеки и очереди. Существует диагональная схема хранения симметричных матриц, а также связные схемы разреженного хранения. Связная схема хранения матриц, предложенная Кнутом, предлагает хранить в массиве (например, в AN) в произвольном порядке сами элементы, индексы строк и столбцов соответствующих элементов (например, в массивах I и J), номер (из массива AN) следующего ненулевого элемента, расположенного в матрице по строке (NR) и по столбцу (NC), а также номера элементов, с которых начинается строка (указатели для входа в строку – JR) и номера элементов, с которых начинается столбец (указатели для входа в столбец – JC). Данная схема хранения избыточна, но позволяет легко осуществлять любые операции с элементами матрицы.
Наиболее широко используемая схема хранения разреженных матриц – это схема, предложенная Чангом и Густавсоном, называемая: "разреженный строчный формат". Эта схема предъявляет минимальные требования к памяти и очень удобна при выполнении операций сложения, умножения матриц, перестановок строк и столбцов, транспонирования, решения систем линейных уравнений, при хранении коэффициентов в разреженных матрицах и т.п.
В этом случае значения ненулевых элементов хранятся в массиве AN, соответствующие им столбцовые индексы – в массиве JA. Кроме того, используется массив указателей, например IA, отмечающих позиции AN и JA, с которых начинаются описание очередной строки. Дополнительная компонента в IA содержит указатель первой свободной позиции в JA и AN.
Разреженный вектор – это разреженная матрица-строка или матрица-столбец, поэтому рассмотрим скалярное умножение разреженных векторов (как частный случай работы с матрицей) с использованием так называемого расширенного массива указателей IP. Например, есть два разреженных вектора a и b размером N. Значения векторов приведены в таблице.
Вектор |
Индекс J |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
a |
|
3 |
1.5 |
|
-0.4 |
|
4.4 |
-8 |
|
|
|
|
|
b |
|
|
1.2 |
-2.2 |
0.4 |
|
|
|
|
|
7 |
|
Представление этих векторов в разреженном строчном формате будет следующим:
Индексы элементов вектора a : JА = 2; 7; 3; 8; 5.
Значения элементов вектора a : AN = 3; 4,4; 1,5 –8; -0,4.
Индексы элементов вектора b : JB = 4; 3; 11; 5.
Значения элементов вектора b : BN = -2,2; 1,2; 7; 0,4.
Данная схема хранения является упакованной, так как хранятся только ненулевые элементы, и неупорядоченной, так как номера индексов могут идти и не по возрастанию (что и показано в данном примере).
Допустим, необходимо вычислить скалярное произведение векторов a и b:
h = 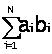
При вычислении стандартным способом нужно N2 просмотров массива. Для сокращения алгебраических операций удобно во время работы хранить расширенный (по размерности массивов a и b) массив указателей IP (его начальное состояние - нулевое). Этот массив заполняется путем одного просмотра массива JA
Алгоритм разреженного вычисления следующий:
1. Просматривается массив JA (первое значение –2) и в соответствующий элемент массива IP (для данного примера – во второй элемент) вписывается индекс массива JA (т.е. –1). Таким образом хранятся указатели позиций ненулевых элементов в АN.
Получается массив указателей IP в виде
1 2 3 4 5 6 7 8 9 10 11 12...
IP 0 1 3 0 5 0 2 4 0 0 0 0,
Где вторая строка – номер индекса в JA.
Отсюда видно, что второй, третий, пятый, седьмой и восьмой элементы исходного массива не являются нулевыми, а хранящийся во втором элементе IP индекс 1 указывает на то, что элемент а2 хранится в первом элементе массива АN(1), а элемент а7 – во втором элементе массива АN (2),
2. Просматривается массив JB. Если соответствующий элемент массива IP ненулевой, т.е. позиции элементов в векторах a и b совпадают, то вычисляются произведения ai * bi и накапливаем в сумму произведений h до тех пор, пока не будет исчерпан массив JB. В результате
JB(1) = 4, IP(4) = 0 - действий нет;
JB(2) = 3, IP(3) = 3.
Следовательно, третий элемент массива AN не является нулевым, т.е. AN(3) = 1,5, а BN(2) = 1,2. Получаем произведение BN(2) * AN(3) = 1,8 и накапливаем результат в сумму произведений h.
Количество операций в данном алгоритме пропорционально числу ненулевых элементов, не считая засылки N нулей в массив IP.
Применение этого алгоритма особенно эффективно в ситуации, когда вектор нужно скалярно умножить на несколько векторов. В этом случае массив IP заполняется только один раз и затем используется для вычисления всех требуемых скалярных произведений. Эта ситуация возникает при необходимости перемножить разреженную матрицу и разреженный вектор.
Задание
Разработать программу умножения или сложения разреженных матриц. Предусмотреть возможность ввода данных с клавиатуры и использования заранее подготовленных данных. Матрицы хранятся и выводятся в форме трех объектов. Величина матриц - любая (допустим, 1000*1000). Сравнить эффективность (по памяти и времени выполнения) стандартных алгоритмов обработки матриц с алгоритмами обработки разреженных матриц при различной степени разреженности матриц.
Примерные варианты заданий приведены в приложении.
Указания к выполнению работы
Все логически завершенные фрагменты алгоритма (ввод, вывод, обработка и т.п.) необходимо оформить как подпрограммы.
При разработке интерфейса программы следует предусмотреть:
· указание формата и диапазона вводимых данных;
· указание операции, производимой программой;
· наличие пояснений при выводе результата;
· указание формата выводимых данных;
· возможность заполнения матриц вручную (даже при большой размерности, например, 1000*1000).
При тестировании программы необходимо:
o проверить правильность ввода;
o проконтролировать правильность вывода данных (т.е. их соответствие требуемому формату);
o проверить правильность выполнения операций;
o обеспечить вывод сообщений при отсутствии входных данных («пустой ввод»);
o обеспечить вывод сообщений при нулевых результате или вывод нулевого результата при ненулевом входе;
o обеспечить возможность ввода данных и вывода результата как при малых матрицах, так и при больших (например, 1000 * 1000);
o сравнить время выполнения стандартного алгоритма обработки матриц и алгоритма обработки разреженных матриц при различной заполненности матриц.
o сравнить объем требуемой памяти для реализации стандартного алгоритма обработки матриц и алгоритма обработки разреженных матриц при различном проценте заполнения матриц.
Следует также протестировать программу при полной загрузке системы, то есть при полном заполнении матриц. Программа должна адекватно реагировать на неверный ввод, пустой ввод и выход за границы матрицы или вектора. Необходимо тщательно следить за освобождением динамической памяти при окончании программы.
Содержание отчета
В отчете по лабораторной работе должен быть сделан вывод, о том, в каких случаях применения какого алгоритма целесообразно для обработки матрицы, какую выгоду дает тот или иной алгоритм. Подтвердить это результатом числовых сравнений расходования памяти и времени выполнения при различной степени разреженности матриц. Обратить особое внимание на тестирование программы.
Отчет по лабораторной работе должен содержать ответы на следующие вопросы:
1. Что такое разреженная матрица, какие схемы хранения таких матриц Вы знаете?
2. Каким образом и сколько памяти выделяется под хранение разреженной и обычной матрицы?
3. Каков принцип обработки разреженной матрицы?
4. В каком случае для матриц эффективнее применять стандартные алгоритмы обработки матриц? От чего это зависит?
Список рекомендуемой литературы
1. Писсанецки С. Технология разреженных матриц.: Пер. с англ. - М.: Мир, 1988.
2. Тьюарсон Р. Разреженные матрицы.: Пер. с англ. М.: Мир, 1977.
Приложение
Примерные варианты заданий
1. Разреженная (содержащая много нулей) матрица хранится в форме трех объектов:
вектора A, содержащего значения ненулевых элементов;
вектора JA, содержащего номера столбцов для элементов вектора A;
связного списка IA, в элементе Nk которого находится номер компонент в A и JA, с которых начинается описание строки Nk матрицы A.
Используя алгоритм обработки разреженных матриц, смоделировать операцию сложения двух матриц, хранящихся в этой форме, с получением результата в той же форме.
Произвести операцию сложения, применяя стандартный алгоритм работы с матрицами. Сравнить время выполнения операций и объем памяти при использовании этих двух алгоритмов
2. Разреженная (содержащая много нулей) матрица хранится в форме трех объектов:
вектора A, содержащего значения ненулевых элементов;
вектора IA, содержащего номера строк для элементов вектора A;
связного списка JA, в элементе Nk которого находится номер компонент в A и IA, с которых начинается описание столбца Nk матрицы A.
Используя алгоритм обработки разреженных матриц, смоделировать операцию сложения двух матриц, хранящихся в этой форме, с получением результата в той же форме.
Произвести операцию сложения, применяя стандартный алгоритм работы с матрицами. Сравнить время выполнения операций и объем памяти при использовании этих двух алгоритмов
3. Разреженная (содержащая много нулей) матрица хранится в форме трех объектов:
вектора A, содержащего значения ненулевых элементов;
вектора JA, содержащего номера столбцов для элементов вектора A;
связного списка IA, в элементе Nk которого находится номер компонент в A и JA, с которых начинается описание строки Nk матрицы A.
Используя алгоритм обработки разреженных матриц, смоделировать операцию умножения, хранящихся в этой форме вектора-строки и матрицы с получением результата в той же форме.
Произвести операцию умножения, применяя стандартный алгоритм работы с матрицами. Сравнить время выполнения операций и объем памяти при использовании этих двух алгоритмов
4. Разреженная (содержащая много нулей) матрица хранится в форме трех объектов:
вектора A, содержащего значения ненулевых элементов;
вектора IA, содержащего номера строк для элементов вектора A;
связного списка JA, в элементе Nk которого находится номер компонент в A и IA, с которых начинается описание столбца Nk матрицы A.
Используя алгоритм обработки разреженных матриц, смоделировать операцию умножения, хранящихся в этой форме матрицы и вектора-столбца с получением результата в той же форме.
Произвести операцию умножения, применяя стандартный алгоритм работы с матрицами. Сравнить время выполнения операций и объем памяти при использовании этих двух алгоритмов.