Этап №7
Обработка деревьев
Цель работы – получить навыки применения двоичных деревьев, реализовать основные операции над деревьями: обход деревьев, включение, исключение и поиск узлов.
Краткие теоретические сведения
Дерево – это нелинейная структура данных, используемая для представления иерархических связей, имеющих отношение «один ко многим».
Дерево с базовым типом Т определяется рекурсивно либо как пустая структура (пустое дерево), либо как узел типа Т с конечным числом древовидных структур этого же типа, называемых поддеревьями.
Деревья используются при построении организационных диаграмм, анализе электрических цепей, для представления синтаксических структур в компиляторах программ, для представления структур математических формул, организации информации в СУБД и, кроме того, для более эффективного извлечения данных.
.Самый верхний узел дерева называется корнем. Верхний узел для нижнего узла называется предком, а нижний узел для верхнего – потомком. Вершины (узлы), не имеющие потомков, называются терминальными вершинами или листьями. Нетерминальные вершины называются внутренними. Две вершины дерева соединяются ветвью. Дерево без ветвей с одной вершиной – это пустое или нулевое дерево.
Корень дерева лежит на нулевом уровне. Максимальный уровень какой-либо вершины дерева называется ее глубиной (от корня до узла) или высотой (от узла до максимально удаленного листа ). Отсюда максимальный уровень корня равен нулю. Максимальный уровень всех вершин называется глубиной дерева.
Число непосредственных потомков у вершины (узла) дерева называется степенью вершины (узла).
Максимальная степень всех вершин является степенью дерева. Число ветвей от корня к вершине есть длина пути к этой вершине.
Каждому узлу дерева можно сопоставить имя узла и значение узла, то есть собственно данные, хранящиеся в этом узле. Причем, если значением являются разнородные данные (записи или объединения), то значением узла можно считать значение одного из полей этих данных, называемого ключом.
Например, есть дерево (рис 1), где номер узла может быть как его именем, так и его значением (в данном случае все равно)
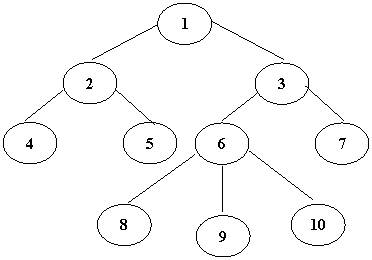

Рис. 1
В памяти деревья можно представить в виде связей с предками (еще их называют родителями); связного списка потомков (сыновей) или структуры данных.
Представление указанного дерева (см. рис 1) в виде связей с предками:
|
№ вершина |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Родитель |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
6 |
6 |
6 |
Пример представления этого же дерева в виде связного списка сыновей приведен на рис 2:
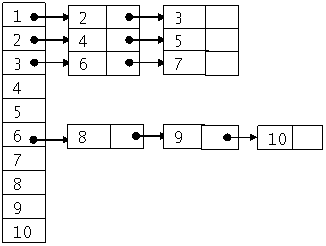
Рис. 2.
Если у каждой вершины дерева имеется не более двух потомков (левые и правые поддеревья), то такое дерево называется двоичным или бинарным.
Двоичные деревья широко используются в программировании.
Основные операции с деревьями: обход дерева, поиск по дереву, включение в дерево, исключение из дерева.
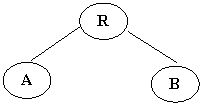 Обход (посещение) вершин дерева можно осуществить
Обход (посещение) вершин дерева можно осуществить
следующим образом (рис 3):
- сверху вниз: R,A,B (префиксный обход)
- слева направо: A,R,B (инфиксный обход)
- снизу вверх: A,B,R (постфиксный обход)
Рис. 3
Для реализации алгоритмов поиска используются деревья двоичного поиска. Дерево двоичного поиска – это такое дерево, в котором все левые потомки моложе предка, а все правые – старше. Это свойство называется характеристическим свойством дерева двоичного поиска и выполняется для любого узла, включая корень. С учетом этого свойства поиск узла в двоичном дереве поиска можно осуществить, двигаясь от корня в левое или правое поддерево в зависимости от значения ключа поддерева.
Если при построении дерева поочередно располагать узлы слева и справа, то получится дерево, у которого число вершин в левом и правом поддеревьях отличается не более чем на единицу. Такое дерево называется идеально сбалансированным.
N элементов можно организовать в бинарное дерево с высотой не более log2(N) , поэтому для поиска среди N элементов может потребоваться не больше log2(N) сравнений, если дерево идеально сбалансировано. Отсюда следует, что дерево – это более подходящая структура для организации поиска, чем, например, линейный список.
Операция включения элемента в дерево разбивается на три этапа: включение узла в пустое дерево, поиск корня для добавления нового узла, включение узла в левое или правое поддерево.
Для удаления узла с указанным ключом сначала происходит его поиск. В случае, если узел найден, то он удаляется. Если удаляемый узел является концевым, то просто удаляется ссылка на него. Если удаляемый узел имеет одного потомка, в этом случае переадресуется ссылка на этого потомка. Если удаляемый узел имеет двух потомков, то на его место ставится самый правый потомок из левого поддерева или самый левый потомок из правого поддерева.
Задание
Построить дерево в соответствии с заданным вариантом задания. Вывести его на экран в виде дерева. Реализовать основные операции работы с деревом: обход дерева, включение, исключение и поиск узлов. Сравнить эффективность алгоритмов сортировки и поиска в зависимости от высоты дерева и степени его ветвления.
Примерные варианты заданий приведены в приложении.
Указания к выполнению работы
Все логически завершенные фрагменты алгоритма (ввод, вывод, обход дерева, включение узла, исключение узла и т.п.) необходимо оформить в виде подпрограмм.
При разработке интерфейса программы следует предусмотреть:
· указание типа, формата и диапазона вводимых данных;
· указание действий, производимых программой;
· наличие пояснений при выводе результата;
· вывод дерева осуществить в графическом виде (или предложить иную визуализацию в виде дерева).
При тестировании программы необходимо:
o проверить правильность ввода и вывода данных (т.е. их соответствие требуемому типу и формату). Обеспечить адекватную реакцию программы на неверный ввод данных;
o обеспечить вывод сообщений при отсутствии входных данных («пустой ввод»);
o проверить правильность выполнения операций;
o обеспечить возможность добавления узла в пустое дерево;
o предусмотреть вывод сообщения при попытке удаления узла из пустого дерева;
o проверить различные варианты включения и исключения узла в существующее дерево;
o проверить поиск существующего узла и поиск несуществующего узла в дереве;
o создать левостороннее или правостороннее дерево, проверить время обработки узла в нем.
Содержание отчета
В отчете по лабораторной работе должны быть сделаны выводы о том, в каких случаях удобно применять деревья, какую выгоду дает использование этого типа данных, какие «узкие места» необходимо протестировать в разработанной программе.
В отчете по лабораторной работе должны быть даны ответы на следующие вопросы:
1. Что такое дерево?
2. Как выделяется память под представление деревьев?
3. Какие бывают типы деревьев?
4. Какие стандартные операции возможны над деревьями?
5. Что такое дерево двоичного поиска?
Отчет представляется в электронном или печатном виде.
Список рекомендуемой литературы
- Вирт Н. Алгоритмы и структуры данных: Пер. с англ. СПб.: Невский диалект, 2001. С. 69–71, 235–258.
2. Ахо А., Хопкрофт Д.,. Ульман Д Структуры данных и алгоритмы: Пер. с англ. М.: Издат. дом «Вильямс», 2000. С. 77–99.
- Иванова Г. С. Основы программирования. М.: Издательство МГТУ им. Н.Э. Баумана, 2001. С. 238–253.
- Керниган Б., Пайк Р. Практика программирования: Пер. с англ. СПб.: Невский диалект, 2001. С. 83–90.
5. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ, Пер. с англ. М.: МЦНМО, 2001. С. 92–97.
Приложение
Примерные варианты заданий
1 Построить двоичное дерево поиска из букв вводимой строки. Вывести его на экран в виде дерева. Выделить цветом все буквы, встречающиеся более одного раза. Удалить из дерева эти буквы. Вывести оставшиеся элементы дерева при постфиксном его обходе. Сравнить время удаления повторяющихся букв из дерева и из строки.
2 Построить двоичное дерево поиска, в вершинах которого находятся слова из текстового файла. Вывести его на экран в виде дерева. Определить количество вершин дерева, содержащих слова, начинающиеся на указанную букву. Выделить эти вершины цветом. Сравнить время поиска слов, начинающихся на указанную букву в дереве и в файле.
3 Построить и вывести на экран бинарное дерево следующего выражения: 9 + 8 * (7 + (6 * (5 + 4) – (3 – 2)) +1)). Написать процедуры постфиксного, инфиксного и префиксного обхода дерева и вывести соответствующие выражения на экран. Подсчитать результат. Используя «польскую» запись, ввести данное выражение в стек. Сравнить время вычисление выражения с использованием дерева и стека.
4 Построить частотный словарь из слов текстового файла в виде дерева двоичного поиска. Вывести его на экран в виде дерева. Осуществить поиск указанного слова в дереве и в файле. Если слова нет, то добавить его при необходимости в дерево и соответственно в файл. Сравнить время поиска в дереве и в файле.