4. Моделирование технологических процессов.

Общие положения .

             Модели технологических процессов могут быть детерминированными и стохастическими .

В детерминированных моделях процесс или действие объекта описывается аналитическими выражениями, чаще всего системами дифференциальных или алгебраических уравнений.

В стохастических моделях процесс или действие объекта описывается стохастическими уравнениями,  и физический смысл имеют не отдельные реализации процесса, а совокупность реализаций и их параметры (математическое ожидание, дисперсия, корреляционные зависимости  и т.д.). Эффективность стохастических моделей в значительной  степени  определяется качественным выполнением всех этапов эксперимента (выдвижение гипотезы, планирование, проведение, обработка  результатов   и т.д.).

            По данным эксперимента определяется зависимость математического ожидания переменной   y  (отклика) от независимых переменных (факторов)  x₁ , x₂ , … , x_m , которые ,как  предполагается ,влияют на объект исследования :

                           y = f (x₁ , x₂ , … , x_m ,  Q₁ , Q₂ , … , Q_m )  ,                                          (4.1)               

где    Q₁ , Q₂ , … , Q_m  - параметры модели .

Выражение  (4.1)  называют функцией отклика .

            В технологических исследованиях  имеются :

            1)  факторы, не допускающие целенаправленного изменения их в ходе исследования

(твердость, состав, структура материала  и т.п.);

            2)  управляемые факторы  , с помощью которых реализуется заданные условия работы объекта ( режимы обработки , характеристики оборудования  и оснастки и т.п.);

            3)   неконтролируемые входные или независимые факторы , характеризующие действующие на объект возмущения (неконтролируемые изменения химического состава , температуры , изменение свойств оборудования и оснастки во времени и т.п.) .

            В функции отклика обычно учитываются только факторы первых двух групп. Действие    неконтролируемых факторов приводит к дрейфу  характеристик объекта  (значение отклика).

            По числу переменных эксперименты разделяют на одно-  и многофакторные : при однофакторных  изменяют и регистрируют один фактор ,при многофакторных  - несколько  факторов (независимых переменных).

            Объекты исследований в эксперименты разделяют на статистические и детерминированные, управляемые и неуправляемые .

            В статистических объектах отклик  y  находится в стохастической связи  с факторами

x₁ , x₂ , … , x_m .

            Для детерминированных объектов характерны функциональные связи между неслучайными величинами.

            Управляемость объекта определяется возможностью воспроизведения на нем результатов опыта .

            Эксперимент, в котором уровни факторов в каждом опыте задаются исследователем,

называют активным , а  в противном случае – пассивным.

            В зависимости от типов переменных, использующихся в модели  (4.1)  и функции отклика ,эксперимент может быть качественным и количественным .По месту проведения эксперимент может быть лабораторным и промышленным. В зависимости от режима реализации различают автоматизированный и неавтоматизированный эксперимент.

            Эксперимент ,в котором реализуются все возможные сочетания уровней факторов ,

называется полным факторным экспериментом. Для двух уровней каждого фактора имеем полный факторный эксперимент типа  2^к , где   к – количество факторов; число необходимых опытов  N=2^к   (табл. 1.2).

таблица 1

полный факторный план для

двух факторов (2² )

номер опыта	x1	x2	y
1 2 3 4	+1 -1 +1 -1	-1 -1 +1 +1	y1 y2 y3 y4

Планируя эксперимент , на 1-ом этапе стремятся получить модель – полином первой степени (линейная модель), хотя нет гарантии ,что при выбранных уровнях варьирования процесс описывается  линейной  моделью.

            Коэффициенты полинома  (линейной модели )

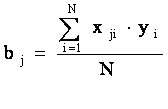       ,  j = 0 , 1 , … , m ,  (4.5) 

     где      b_j – коэффициент модели с номером  j  ;

x_ji – значение j-ого фактора в i-м опыте плана ;

y_i  - значение функции отклика   в i- м опыте плана ;

  Таблица 2

номер опыта	x1	x2	x3	y	номер опыта	x1	x2	x3	y
1 2 3 4	+1 +1 +1 +1	+1 +1 -1 -1	+1 -1 +1 -1	y1 y2 y3 y4	5 6 7 8	-1 -1 -1 -1	+1 +1 -1 -1	+1 -1 +1 -1	y5 y6 y7 y8

   Полный  факторный план для трех факторов (2²)

N- количество опытов в плане .  

           Соответствие полученной математической модели процесса экспериментальным данным называется адекватностью. Уравнение  адекватно описывает  результаты опытов , если квадратическое отклонение значений зависимой переменной ,рассчитанных по модели (y_Мi),

от экспериментальных данных (y_i) обусловлено только ошибкой воспроизведения , т.е. случайным  характером этого параметра. Проверку на адекватность см. в

Если линейная модель неадекватна ,то рассматривают модели ,учитывающие взаимодействие факторов (табл. 3) , для чего пользуются правилом перемножения столбцов.

Таблица 3

Полный факторный план для двух факторов

с учетом их взаимодействия 

№ опыта	x1	x2	x1x2	y
1 2 3 4	+1 +1 -1 -1	+1 -1 +1 -1	+1 -1 -1 +1	y1 y2 y3 y4

Иные типы планов, а также планы для другого числа факторов приведены в

Методы планирования эксперимента .

До проведения эксперимента необходимо установить интервалы между значениями факторов, прежде всего независимых.

            Однофакторный эксперимент бывает двух типов: последовательный  рандомизированный.

            При последовательном эксперименте уровень фактора изменяется скачкообразно (по шагам). После каждого шага оценивается результат и принимается решение о ходе дальнейшей  работы. Последовательный эксперимент целесообразен:

            1)  если известно, что он  невоспроизводим (при испытании образца на растяжение нагрузка меняется ступенчато , в образце после первого же приложения нагрузки происходят

происходят необратимые изменения) ;

            2) если особенности объекта можно выявить только при получении данных в регулярной последовательности  (анализ стабильности технологического процесса обработки).

            В рандомизированном  эксперименте уровень фактора меняется случайным образом с целью сведения эффекта некоторого неучтенного неслучайного фактора к случайной ошибке.

            Наиболее часто при описании технологических процессов  ,и в первую очередь ,когда природа физических явлений ,их сопровождающих ,не ясна используют полиномиальные модели:

            -  полином первой степени  

            - полином второй степени    

            Соответственно этому планы экспериментов,  цель которых- отыскание модели процесса в виде полинома первой или второй степени , называют планами второго и первого порядков.

            На первом этапе планирования выбираются условия эксперимента :

            1)  определяется область экспериментирования -  границы изменения независимых факторов;

2) устанавливается второй основной уровень исследуемых факторов;

            3) устанавливаются интервалы варьирования;

            4) определяется точность фиксирования факторов.

            Основным уровнем называют центр  исследуемой области изменения данного фактора. Обычно 

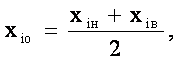                                     (4.2)

где     x _{i , 0 , Н, В}    -соответственно значения основного ,нижнего и верхнего уровней фактора   x_i .

Интервалом варьирования факторов  I_i называется число (свое для каждого фактора) ,  прибавление которого к основному уровню дает верхний , а вычитание – нижний уровень фактора:

                (4.3)              

         Для упрощения  записи условий эксперимента  и обработки экспериментальных данных масштабы по осям выбираются так , чтобы верхний уровень соответствовал  +1 ,а основной – нулю.

            Это можно сделать с помощью преобразований

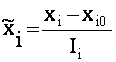,                                                                   (4.4)

где    x_i -натуральное значение фактора ;

x _io - натуральное значение основного уровня ;

I_i      -интервал варьирования ;

     - кодированное значение фактора.

Например, в эксперименте скорость резания изменяется от 40 м/мин до 160 м/мин.Тогда

x _{i Н}      = 40 м/мин  ;   x _{i В}     = 160 м/мин ;     x _io = (40+160)/2=100 м/мин;

I_i =60 м/мин ; =(40-100)/60 = -1 ; =0 ;         =+1 .

            Точность фиксирования уровней фактора считается высокой, если погрешность измерения более 1 %, средней – не более 5% . В технологических исследованиях  погрешность измерения может иногда достигать 20% .

            Применение КРА правомерно и эффективно ,если :

            а) зависимая переменная y- случайная величина с нормальным законом распределения;

б) дисперсия y не зависит от абсолютных значений y;

в) значение  x₁ , x₂ , … , x_m изменяются с ошибками  , пренебрежимо малыми по сравнению с  y ;

            г) переменные    x₁ , x₂ , … , x_m линейно независимы  ;

            д) процесс изменения y является стационарным и случайным ;

е) экспериментальные данные получены из ряда независимых испытаний и образуют случайную выборку из данных генеральной совокупности.

            Условия   “а – г ”  проверяются для активного и пассивного экспериментов ,условия

“ д  ”  и    ” е  ”  - для пассивного эксперимента [ 15 ].

            Для вычисления коэффициентов управления регрессии используют метод наименьших квадрантов (МНК). Коэффициенты регрессии , найденные с помощью МНК ,обеспечивают минимкм суммы квадрантов отклонений опытных данных   y_i от значений вычисленных по уравнению регрессии       , т.е. минимум функций

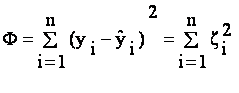, где  (4.11)

Для линейной однофакторной зависимости  выполнено n опытов,

в   результате которых имеем систему :

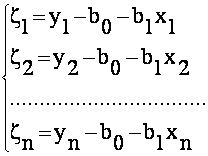 (4.12)

Система  (4.12)  является переопределенной (n>2) и ,возможно, несовместимой . Найти 

неизвестные коэффициенты  b₀   и  b₁   можно из условия  

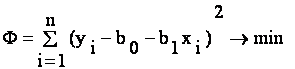 (4.13)

Если  минимум    Ф    существует , то

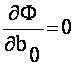
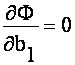
Выполнение этой процедуры дает возможность составить систему линейных уравнений ,в

которой число уравнений равно числу неизвестных . Окончательно

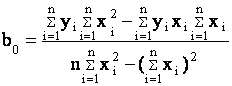                             (4.14)

.

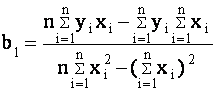Корреляционно-регрессивный анализ.

Для  получения математических моделей статистических объектов исследования , весьма характерных для технологических исследований ,зачастую эффективно применение корреляционно- регрессивного  анализа   (КРА). Методы КРА применимы только для взаимосвязанных факторов.

На первом этапе КРА оценивают степень взаимосвязи значений функции отклика y

с одной или несколькими независимыми переменными   x₁ , x₂ , … , x_m . В первом случае используется коэффициент парной   (r_yx) , во втором – коэффициент множественной

( R_y,x1,x2,xm)  корреляции :

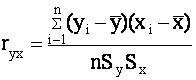,                                                (4.6)

где  - средние арифметические  значения   y _n ,x _i в рассматриваемой выборке ;

n – число измерений (объем выборки );

S_x , S_y - среднее квадратическое отклонение   x _i и  y .

При этом

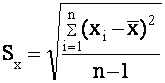        ;             если   n>30 , то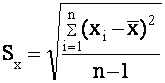    

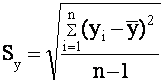        ;             если   n>30 , то  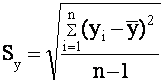          (4.7)

Обозначив зависимую переменную цифрой 1 , а независимую(ые) – цифрами   2,3,4 …..m,

получим обозначение коэффициентов парной корреляции    r₁₂  , r_{13 , … ,} r_1m  ;

коэффициентов  множественной корреляции между   y  и   x₁ , x₂ , … , x_m - R_{1,2,3,4,…,m  .}

Тогда

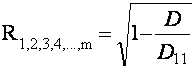 ,                                                               (4.8 )

где  D – определитель , составляемый из всех коэффициентов парной корреляции

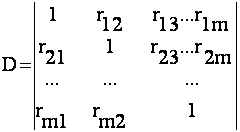;                                                                       (4.9)

D₁₁ – определитель ,получаемый вычеркиванием из D первого слева столбца и верхней строки .

В случае трех переменных

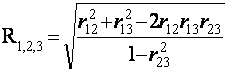.                                                     (4.10)

Значение  r_yx  и     R_y,x1,x2,xm находятся в пределах   -1…+1 . Если они существенно отличаются от нуля ,то между исследуемыми факторами существует линейная корреляционная    зависимость. В  противном случае эта зависимость отсутствует или является существенно нелинейной.  Если     r_yx  или    R_y,x1,x2,xm равны   +1  или   -1 ,то между исследуемыми факторами  существует  функциональная связь. Знаки    r_yx  или    R_y,x1,x2,xm говорят о прямом  (знак “+”)   или обратном   (знак “-”)    характере взаимосвязи между факторами .

Если корреляционные связи между факторами существуют ,то с помощью регрессивного анализа выбирают математическую модель ,наилучшим образом описывающую указанные взаимосвязи .  Уравнение , по которому могут быть найдены числовые значения выборочных средних функций отклика (y)  при независимых переменных (x₁ , x₂ , … , x_m ),

называется уравнением регрессии.