ПЛОСКОСТЬ

      Плоскость - неопределяемое понятие геометрии.
      В пространстве плоскость может быть задана (рис.1):
      тремя точками, точкой и прямой, двумя параллельными прямыми, двумя пересекающимися прямыми (в частном случае, горизонталью и фронталью или двумя следами), отсеком плоской фигуры.
      На комплексном чертеже положение плоскости, как правило, вполне определяется проекциями указанных фигур (рис.2а, рис.3а, рис.4а).

Теорема. A М a Ы A' М aa' Щ A" М aa"       Если точка принадлежит плоскости, то проекции точки принадлежат одноименным проекциям прямой, лежащей в этой плоскости (рис.3б).

      Главные линии плоскости

      Линии уровня плоскости - прямые, принадлежащие плоскости и параллельные какой-либо плоскости проекций (рис.2б и рис.3а):
      h_a - горизонталь плоскости a : h_a || p₁ Ю h_a" || x ;
      f_a - фронталь плоскости a : f_a || p₂ Ю f_a' || x .
      Следы плоскости - прямые, по которым данная плоскость пересекается с плоскостями проекций (рис.4а):
      h_0a - горизонтальный след плоскости a ("нулевая горизонталь"):       h_0a = a З p₁ Ю h_0a" є x ;
      f_0a - фронтальный след плоскости a ("нулевая фронталь"):
      f_0a = a З p₂ Ю f_0a' є x ;
      Линия наибольшего наклона плоскости к горизонтальной плоскости проекций - прямая, принадлежащая данной плоскости и перпендикулярная к ее горизонтали (линия q_a на рис.1).
      Линия наибольшего наклона плоскости к фронтальной плоскости проекций - прямая, принадлежащая данной плоскости и перпендикулярная к ее фронтали (линия u_a на рис.1).



      Плоскость общего положения - плоскость, произвольно наклоненная к плоскостям проекций (рис.1).
      Плоскости уровня - плоскости, параллельные какой-либо плоскости проекций:
      b - горизонтальная плоскость (рис.5а):
      b || p₁ Ю f_0b || x ;
      g - фронтальная плоскость (рис.5б):
      g || p₂ Ю h_0g || x .
      Проецирующие плоскости - плоскости, перпендикулярные к какой-либо плоскости проекций:
      d - горизонтально проецирующая плоскость (рис.5в):
      d ^ p₁ Ю f_0d ^ x ;
      l - фронтально проецирующая плоскость (рис.5г):
      l ^ p₂ Ю h_0l ^ x .
      Фигуры, принадлежащие проецирующей плоскости, проецируются на ее след (прямую) - вырожденную проекцию на одноименную плоскость проекций (рис.5в и рис.5г).

      Метрические характеристики фигур плоскости

Правило определения угла наклона y° плоскости общего положения к какой-либо плоскости проекций (рис.4б).       1. Провести линию наибольшего наклона (ЛНН) к одноименной линии уровня.       2. Определить угол наклона j° построенной ЛНН к выбранной плоскости проекций.       3. Построенный угол для ЛНН равен углу наклона самой данной плоскости к выбранной плоскости проекций (j ° = y°).

      Основные понятия:
      Плоскость
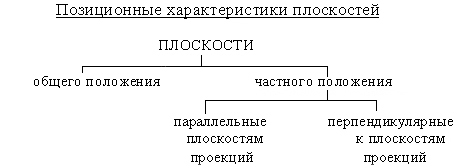
      Плоскость общего положения
      Плоскости частного положения: плоскости уровня, проецирующие плоскости
      Линии уровня плоскости: горизонталь плоскости, фронталь плоскости
      Следы плоскости
      Линии наибольшего наклона плоскости