ПОВЕРХНОСТИ
Поверхность - множество положений движущейся в пространстве линии(рис.1).
Поверхность - двупараметрическое множество точек.
Поверхность считается полностью заданной, а чертеж поверхности метрически определенным, если могут быть построены проекции любой точки, принадлежащей поверхности. Основой для ее построения служит теорема о принадлежности.
|
Теорема: А М a Ы А' М la' Щ А" М la" Если точка принадлежит поверхности, то проекции точки принадлежат соответствующим проекциям линии, лежащей на поверхности. |
Образующая - линия (прямая или кривая), которая при своем движении образует какую-либо поверхность.
Движение образующей может быть задано:
- направляющими линиями,
- законом перемещения образующей, а именно:
. параллельным переносом (сдвигом);
. вращением;
. винтовым движением (композицией сдвига и вращения).
Направляющие - линии (прямые или кривые), задающие направление движения образующей.
Определитель - необходимое и достаточное множество геометрических фигур (Г) и связей между ними [A], которые однозначно задают поверхность.
Общая структура определителя имеет вид:
F (G) ; [A], где:
F - обозначение поверхности (как геометрической фигуры);
(G) - геометрическая часть; [A] - алгоритмическая часть определителя.
На комплексном чертеже поверхность может быть задана проекциями геометрических фигур определителя, каркасом или очерком.
Каркас - упорядоченное множество точек или линий, принадлежащих поверхности.
Очерк - границы видимости поверхности по отношению к плоскостям проекций.
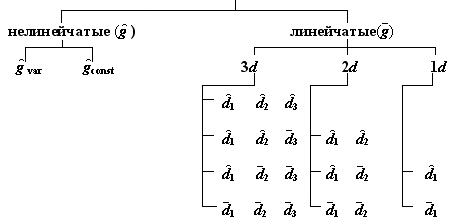
Классификация
по виду образующих и направляющих
ПОВЕРХНОСТИ

где:
![]() - криволинейная образующая переменного вида;
- криволинейная образующая переменного вида;
![]() - криволинейная образующая постоянного вида;
- криволинейная образующая постоянного вида;
![]() - прямолинейная образующая;
- прямолинейная образующая;
![]() - криволинейная направляющая;
- криволинейная направляющая;
![]() - прямолинейная направляющая.
- прямолинейная направляющая.
Нелинейчатыми называют поверхности, образующая которых - кривая линия, изменяющая свою форму по мере перемещения (![]() ) или сохраняющая ее (
) или сохраняющая ее (![]() ).
).
Линейчатыми называют поверхности, которые могут быть образованы движением прямой образующей ![]() .
.
Из поверхностей с двумя направляющими выделим группу, называемую поверхностями с плоскостью параллелизма. Их общий признак: образующая при своем движении параллельна некоторой плоскости, называемой плоскостью параллелизма.
Их определитель:
![]() .
.
В зависимости от формы направляющих (прямые или кривые) наиболее распространенными представителями этого семейства являются:
- цилиндроид (обе направляющие - кривые);
- коноид (одна направляющая - кривая, другая - прямая);
- косая плоскость или гиперболический параболоид (обе направляющие - прямые) (рис.2).
Из группы поверхностей с одной направляющей отметим коническую и цилиндрическую поверхности.
Цилиндрическая поверхность образована движением прямой образующей по одной направляющей при условии параллельности всех образующих (рис.3).
Коническая поверхность образована движением прямой образующей по одной направляющей при условии пересечения всех образующих в некоторой общей точке - вершине (рис.4).
Классификация
по закону движения образующей
ПОВЕРХНОСТИ
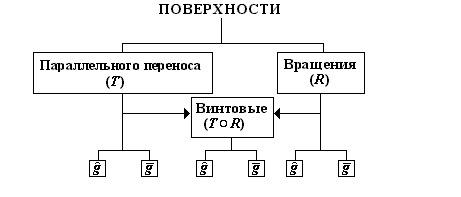
где:
Т - символ параллельного переноса;
R - символ вращения;
o - символ композиции движений;
![]() - криволинейная образующая;
- криволинейная образующая;
![]() - прямолинейная образующая.
- прямолинейная образующая.
Поверхности параллельного переноса
Поверхность параллельного переноса (сдвига) создается движением образующей g вдоль оси переноса i (рис.5).
Поверхности вращения
Поверхность вращения создается вращением образующей (прямой или кривой) вокруг оси вращения (рис.6), где:
i - ось вращения;
g - образующая;
p - параллель поверхности (окружность);
e - экватор (параллель максимального диаметра в своей окрестности);
q - горло (параллель минимального диаметра в своей окрестности);
m - меридиан;
m0 - главный меридиан.
Поверхности вращения с прямой образующей
В зависимости от положения прямой образующей относительно оси вращения можно выделить следующие виды поверхностей этой группы:
- цилиндрические (g || i) (рис.7а);
- конические (gЗi =S) (рис.7б);
- однополостный гиперболоид вращения (g ![]() i) (рис.7в).
i) (рис.7в).
Поверхности вращения с образующей - окружностью
В зависимости от соотношения величин радиуса r окружности и расстояния d от ее центра до оси вращения можно выделить следующие виды поверхностей этой группы:
- закрытый тор (d < R) (рис.8);
- сфера ("вырожденный" тор) (d = 0) (рис.9);
- открытый тор (d > R) (рис.10).
Поверхности вращения с образующей - кривой второго порядка
В зависимости от вида образующей можно выделить следующие виды поверхностей этой группы:
- эллипсоид вращения (рис.11);
- параболоид вращения (рис.12);
- гиперболоид вращения (рис.13).
Винтовые поверхности
Винтовые поверхности (геликоиды) создаются при винтовом движении образующей (прямой или кривой) вокруг оси.
В зависимости от положения прямой образующей по отношению к оси различают следующие виды геликоидов:
- открытый (g ![]() i) , закрытый (g З i);
i) , закрытый (g З i);
- прямой (g ^ i) , наклонный (<g,
i> №
0 ).
На рис.14 дан пример изображения на комплексном чертеже прямого закрытого геликоида.
Основные понятия:
Поверхность
Образующая
Направляющие
Очерк
Каркас
Определитель
Плоскость параллелизма
| Поверхность - множество положений движущейся в пространстве линии. |
| Образующая - линия (прямая или кривая), которая при своем движении образует какую-либо поверхность. |
| Направляющие - линии (прямые или кривые), задающие направление движения образующей. |
| Определитель - необходимое и достаточное множество геометрических фигур и связей между ними, которые однозначно задают поверхность. |
| Каркас - упорядоченное множество точек или линий, принадлежащих поверхности. |
| Очерк - границы видимости поверхности по отношению к плоскостям проекций. |
| Плоскость параллелизма - плоскость, параллельно которой в пространстве движется образующая. |