Лабораторная работа № 1.
Структурный и кинематический анализ рычажных механизмов.
Цель и задачи работы : изучение основных положений и принципов структурного анализа плоских рычажных механизмов; знакомство с правилами составления структурных схем механизмов, условными обозначениями их элементов по ГОСТ-2.770-68, классификацией механизмов по Ассуру; проведение структурного анализа для заданного рычажного механизма, проверка правильности выполненного анализа на ЭВМ.
- Основные положения и понятия структурного анализа механизмов. Механизм — система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемые движения других твердых тел. Звено — твердое тело или система жестко связанных твердых тел, входящая в состав механизма. Все механизмы можно рассматривать как пространственные. Некоторые механизмы можно рассматривать и как плоские. Плоским называется механизм, звенья которого совершают движения в плоскостях, параллельных какой-либо одной плоскости. Движения звеньев механизма рассматривается в системе координат, связанной с одним из звеньев механизма. Это звено называется стойкой и принимается за неподвижное. Входное звено — звено, которому сообщается исходное движения; выходное — выполняет требуемое движение. Соединение двух соприкасающихся звеньев, допускающее их вполне определенное относительное движение, называется кинематической парой.
Кинематические пары классифицируются по следующим признакам:
- виду контакта звеньев — на высшие (с контактом звеньев по линии или точке), и низшие (с контактом звеньев по поверхности);
- характеру относительного движения звеньев. Низшие КП подразделяются на вращательные, поступательные и винтовые;
- числу связей, наложенных КП на относительное движение звеньев (КП 1...5 классов);
- числу подвижностей в относительном движении звеньев КП — на кинематические пары с 1...5 подвижностями.
Например, вращательная и поступательная КП являются низшими одноподвижными парами 5-го класса.
При проведении теоретических и экспериментальных исследований пользуются различными расчетными схемами и моделями механизмов и машин. Они обычно отражают только те свойства механизмов и машин, которые существенно влияют на исследуемые характеристики. Так, при анализе структуры механизма используют его структурную схему; при анализе кинематики — кинематическую; динамики — динамическую. Структурная схема механизма должна содержать информацию о числе его звеньев и их взаимном расположении, виде расположении и классе (или числе подвижностей) кинематических пар. Структурную схему механизма вычерчивают по определенным правилам с использованием условных обозначений, регламентированных ГОСТ 2.770-68. Некоторые обозначения, необходимые для выполнения данной работы, приведены в табл.1.1.
Графическое изображение элементов структурных схем
Таблица 1.1
| Наименование | Графическое изображение | ||||
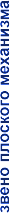 |
Ползун Втулка Поршень Камень |
  |
|||
|
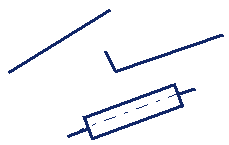
Кривошип Шатун Коромысло Кулиса |
  |
||||
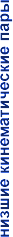 |
Вращательные |
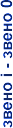 |
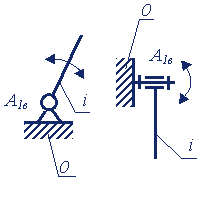 |
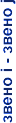 |
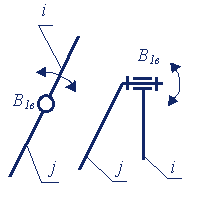 |
| Поступательные |
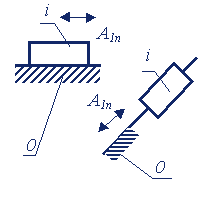 |
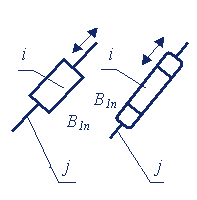 |
|||
Функциональные возможности механизма, в первую очередь, обусловлены числом подвижностей W , т.е. числом независимых обобщенных координат, однозначно определяющих положение всех звеньев механизма в пространстве. При подсчете W можно рассматривать механизм как пространственный и использовать формулу Сомова- Малышева:
W пр =![]()
![]() (1.1)
(1.1)
где n=(k-1) — число подвижных звеньев механизма; k — общее число звеньев (вместе со стойкой); i — число подвижностей в КП; pi — число КП с i подвижностями в механизме.
Если движение звеньев механизма происходит в параллельных плоскостях, то его можно рассматривать как плоский. В этом случае подвижность определяют по формуле Чебышева:
W пл =![]() . (1.2)
. (1.2)
При расчете подвижности механизма в пространстве необходимо учитывать, что при переходе от плоского представления механизма к пространственному число подвижностей каждого звена увеличивается с трех до шести. При этом подвижность некоторых пар может увеличиться. Так в плоском механизме сферические и цилиндрические пары относятся к одноподвижным низшим. В пространственном они становятся: сферическая – трехподвижной, цилиндрическая – двухподвижной.
Большинство механизмов, применяющихся в современных машинах, имеет одну подвижность. При этом достаточно задать движение одному звену для осуществления вполне определенного движения всех остальных. Механизм с W>1 используют реже. Для многих механизмов при расчете по формуле (1.1) получают отрицательное значение или нуль. Однако анализ движения рассматриваемого механизма показывает, что число его подвижностей равно единице. Такое расхождение возникает, если в схеме механизма имеются повторяющиеся или избыточные связи.
Избыточными называют такие связи в механизме, которые дублируют уже имеющиеся и не изменяют его реальной подвижности. Их вводят в структуру механизма с целью повышения его жесткости и точности. Число избыточных связей q в механизме можно определить после задания его подвижности W0 (часто W0=1):
q = W0 - W пр . (1.3)
Величина q определяет степень статической неопределимости механизма при силовом расчете.
1.2. Классификация рычажных механизмов по Ассуру.
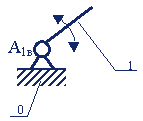
Для плоских механизмов с низшими КП Ассуром Л.В. была разработана система классификации, в которой механизмы состоят из первичных механизмов и структурных групп Ассура (групп нулевой подвижности). Первичным механизмов (рис.1) называют механизм, состоящий из двух звеньев: 1, 0 (одно из них неподвижное — стойка), которые образуют одноподвижную пару (вращательную или поступательную).
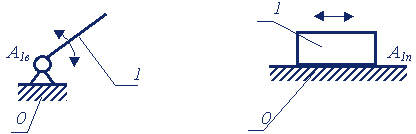
Рис.1.1
Структурная группа, или группа Ассура — кинематическая цепь, которая состоит из подвижных звеньев, соединенных между собой низшими одноподвижными КП, и имеет число подвижностей группы (на плоскости), равное нулю. Звено группы Ассура, входящее в две кинематические пары, одна из которых имеет свободный элемент звена (табл.1.2, пунктирные линии), называется поводком. При синтезе механизма группа присоединяется поводками к звеньям исходного механизма. Если поводки группы присоединить свободными элементами КП к стойке, то образуется плоская статически определимая ферма q грпл =0 и
W грпл =3n гр -2p гр =0 . (1.4)
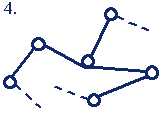
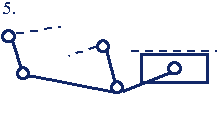
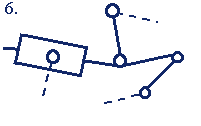
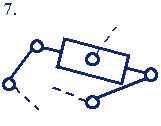
Из выражения (1.4) получают соотношение между числом звеньев и числом КП для групп Ассура n гр =(2/3)p гр. При решении этого уравнения в целых числах определяют параметры групп Ассура: 1-го класса 2-ого порядка — n гр =2, p гр =3 (двухповодковые группы); 1-го класса 3-ого порядка — n гр =4, p гр =6 (трехповодковые группы) и т.п.
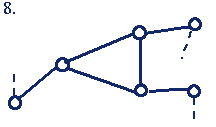
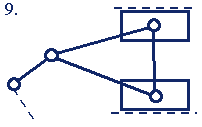
Сложная группа Ассура не может быть образована комбинацией простых групп более низкого класса или порядка. Некоторые примеры групп Ассура 1-го класса 2-го и 3-го порядков приведены в табл.1.2.
При структурном анализе механизма по Ассуру находят количество первичных механизмов и звенья, образующие их, вид и класс групп Ассура, входящих в его состав. Число первичных механизмов, входящих в состав анализируемого механизма, равно подвижности W пл. После выделения звеньев, образующих первичные механизмы, определяют состав и вид групп Ассура, анализируя оставшиеся звенья, начиная со звеньев, наиболее удаленных от первичных механизмов. Звенья объединяют в группу Ассура и мысленно удаляют ее из схемы механизма. При этом оставшиеся звенья образуют механизм с тем же числом подвижностей W пл и не изменяют характера своего движения.
Структурные группы Ассура.
Таблица 1.2.
|
Группы Ассура 1-го класса 2-го порядка (2-го класса 2-го порядка)* |
||
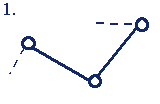
|

|
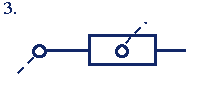
|
|
Группы Ассура 1-го класса 3-го порядка (3-го класса 3-го порядка)* |
||
|
|
|
|
|
|
* в скобках указан класс и порядок группы по классификации И.И.Артоболевского
1.3. Пример структурного анализа рычажного механизма .

На рис. 1.3 изображена структурная схема плоского рычажного восьмизвенного механизма, где арабскими цифрами (от 0 до 7) обозначают звенья, причем символом "0" — стойку; прописными латинскими бувами — кинематические пары.
Структурный и кинематический анализ рычажного механизма .
Таблица 1.3.
|
Движение |
плоское |
2 |
3 |
6 |
||||
|
звена |
вращательное |
1 |
4 |
5 |
7 |
|||
|
механизма |
поступательное |
|||||||
|
Траектории |
прямая |
|||||||
|
центров |
окружность |
B |
D |
E |
||||
|
подвижных шарниров |
сложная кривая |
C |
L |
|||||
|
Число звеньев |
общее |
k=8 |
||||||
|
механизма |
подвижных |
n=7 |
||||||
|
Число и вид кинематических пар |
вращат. |
p 1в =9 |
||||||
|
плоского механизма |
поступ.(цилиндр.) |
p 1п =1(1) |
||||||
|
Число подвижностей |
на плоскости |
W пл =1 |
||||||
|
механизма |
в пространстве |
W пр =-7 |
||||||
|
Заданная подвижность механизма |
W0=1 |
|||||||
|
Число избыточных связей |
q=8 |
|||||||
При анализе механизма необходимо определить:
характер движения его звеньев — вращательное, поступательное или плоское;
траектории центров подвижных шарниров — прямая, окружность или сложная кривая;
общее число звеньев механизма k и число подвижных звеньев n;
число КП — для плоского механизма - вращательных и поступательных; для пространственного – указать пары изменившие подвижность (в анализируемой модели пара L из одноподвижной поступательной в плоском механизме превращается в двухподвижную цилиндрическую в пространственном) ;
число подвижностей на плоскости W пл и в пространстве W пр ;
число избыточных связей q при заданной подвижности W0.
Результаты этого этапа структурного анализа для механизма, представленного на рис.1.2, приведены в табл.1.3.
Далее необходимо провести структурный анализ плоского механизма по Ассуру. Для этого определяют, из каких групп Ассура и первичных механизмов состоит анализируемый механизм, а также его класс и порядок. Класс и порядок механизма соответствуют классу и порядку наиболее сложной группы Ассура, входящей в его состав.
Результаты структурного анализа механизма и анализа групп Ассура приведены в табл.4. В ней указано: число звеньев и КП в группе Ассура или первичном механизме, число подвижностей W грпл и W грпр, число избыточных связей q гр .
Структурный анализ механизма по Ассуру .
Таблица 1.4
|
Схема первичного механизма |
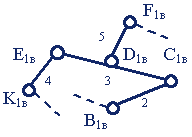
Схема структурной группы |
Схема структурной группы |
||||||||||||
|
|
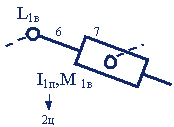
|
||||||||||||
|
Число звеньев в механизме |
2 |
Число звеньев в группе |
4 |
Число звеньев в группе |
2 |
|||||||||
|
Число КП в механизме |
1 |
Число КП в группе |
6 |
Число КП в группе |
3 |
|||||||||
|
Класс |
1 |
Порядок |
1 |
Класс |
1 |
Порядок |
3 |
Класс |
1 |
Порядок |
2 |
|||
|
Подвижность механизма |
W пл =1 W пр =1 |
Подвижность группы |
W грпл =0 W грпр =-6 |
Подвижность группы |
W грпл =0 W пр =-2 |
|||||||||
|
Избыточные связи |
q м =0 |
Избыточные связи |
q гр =6 |
Избыточные связи |
q гр =2 |
|||||||||
Эти величины рассчитывают по формулам:
W грпл =![]() (1.5)
(1.5)
W грпр =![]() (1.6)
(1.6)
q гр = - W грпр (1.7)
Вывод: Рассмотренный одноподвижный восьмизвенный плоский рычажный механизм с низшими КП состоит из одного первичного механизма и двух групп Ассура (одной двухповодковой и одной трехповодковой) и является по классификации Ассура механизмом первого класса третьего порядка (по классификации Артоболевского – механизмом третьего класса).
1.4.Порядок выполнения работы.
1. Ознакомьтесь с заданной моделью рычажного механизма, выделите в нем стойку, определите число и вид КП.
2.Вычертите в журнале структурную схему механизма, используя условные обозначения элементов кинематических схем; отметьте круговой стрелкой входное звено механизма (звено, соединенное с рукояткой модели); обозначьте на схеме звенья (цифрами) и кинематические пары (латинскими буквами).
3. Подсчитайте число звеньев механизма k и n , число вращательных p1в, поступательных p1п и цилиндрических p1ц кинематических пар. Определите по формулам (1.1 ... 1.3) подвижности механизма на плоскости W пл и в пространстве W пр, число избыточных связей q при W0=1. Проанализируйте движение звеньев, механизма, учитывая, что, если звено:
образует со стойкой вращательную КП, то оно совершает вращательное движение, и все его точки движутся по окружности;
образует со стойкой поступательную КП, то оно совершает поступательное движение, и все его точки движутся по прямым;
не образует КП со стойкой, то оно совершает в общем случае плоское движение, и все его точки движутся по некоторым сложным кривым.
Занесите результаты анализа в таблицу журнала.
3. Используя правила и определения, проведите структурный анализ механизма по Ассуру. Проанализируйте первичный механизм и структурные группы, результаты анализа занесите в таблицы журнала.
4. Введите в компьютер программу " LAB 1". Действуя по инструкциям программы, выберите из структурных схем механизмов, предложенных программой, схему заданного Вам механизма. Введите принятые Вами обозначения КП и звеньев, заполните на экране дисплея табл.1.3. После правильного заполнения этой таблицы, перейдите к структурному анализу механизма по Ассуру. Для этого по запросу программы, используя номера структурных групп из табл.1.2, введите в ЭВМ номера групп Ассура, входящих в анализируемый механизм, в порядке их возрастания. Заполните на экране табл.1.4 для первичного механизма и групп Ассура. После сообщения программы о правильном выполнении всех операций, перейдите к п.5.
5. Сформулируйте выводы по работе, укажите в них класс и порядок проанализированного механизма (по классификации Ассура или Артоболевского), перечислите образующие его группы Ассура.