|
ЛЕКЦИЯ 15 |
|
|
Краткое содержание:
Сложные зубчатые механизмы
Механизмы, в которых кинематические
цепи образуют один или несколько замкнутых контуров и в которых входной поток
механической мощности в процессе передачи и преобразования делится на несколько
потоков, а затем суммируется на выходном звене, называются многопоточными механизмами.
Распределение передаваемых усилий по нескольким кинематическим парам уменьшает
нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры
и массу механизмов. Многозонный контакт звеньев механизма существенно увеличивает
жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый
ход и кинематическую погрешность механизма. Однако, за счет образования в структуре
механизма внутренних контуров, число избыточных или пассивных связей в механизме
увеличивается. Поэтому при изготовлении и сборке механизма необходимо либо повышать
точность деталей, либо увеличивать зазоры в кинематических парах.
Сложные зубчатые
механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными
механизмами. К типовым планетарным механизмам относятся:
В таблице 15.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.
Типовые планетарные механизмы
| № | Структурная схема механизма |
Uред
|
КПД
|
|
1
|
 |
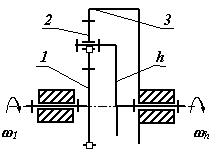3....10 |
0.97....0.99 |
|
2
|
 |
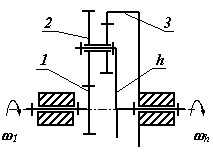7....16 |
0.96....0.98 |
|
3
|
 |
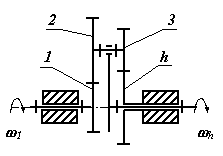25....30 |
0.9....0.3
|
|
4
|
 |
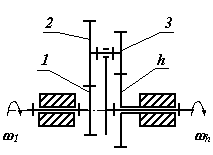30....300 |
0.9....0.3
|
Кинематика рядного зубчатого механизма.
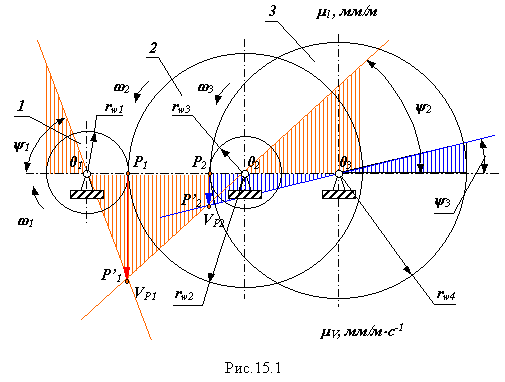
Рядным зубчатым механизмом называется сложный зубчатый механизм с неподвижными осями колес, образованный последовательным соединением нескольких простых зубчатых механизмов. Рассмотрим кинематику рядного механизма составленного из двух зубчатых передач: одной внешнего зацепления и одной внутреннего зацепления. Схема механизма изображена на рис. 15.1.
Напоминание: Для вращательного движения твердого тела относительно оси проходящей через точку А. Примем для размеров масштаб ml, мм/м, а для линейных скоростей - масштаб mV, мм/мЧс-1. Угловая скорость звена i равна
 |
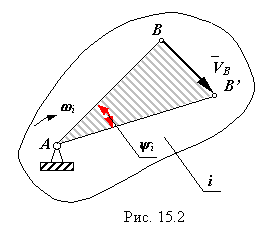Таким образом при графическом кине матическом анализе угловая скорость звена равна произведению тангенса угла наклона прямой распределения лиейных скоростей на отношение масштабов длин и скоростей. |
Аналитическое исследование кинематики рядного механизма
Из основной теоремы зацепления, для первой пары зубчатых колес с внешним зацеплением, можно записать
для второй пары зубчатых колес с внутренним зацеплением
Передаточное отношение механизма в целом будет равно:
Передаточное отношение сложного рядного зубчатого, образованного из нескольких соединенных последовательно простых зубчатых механизмов равно произведению передаточных отношений этих механизмов.
Графическое исследование кинематики рядного механизма
Изобразим в масштабе ml, мм/м, кинематическую схему рядного зубчатого механизма. Нанесем на эту схему линейную скорость точки P1, изобразив ее в произвольном масштабе mV, мм/мЧс-1 отрезком Р1Р'1. Соединим конец этого отрезка точку Р'1 с центрами вращения колес 1 и 2 точками 01 и 02 и получим прямые, определяющие распределение линейных скоростей этих звеньев, для точек лежащих на линии центров. Эти прямые образуют с линией центров соответственно углы y1 иy2 . Точка Р2 является точкой касания начальных окружностей колес 3 и 4. Так как в точке касания начальных окружностей линейные скорости звеньев 2 и 3 равны, а распределение линейных скоростей по линии центров для звена 2 известно, то можно определить отрезок Р2Р'2,который изображает скорость точки Р2 в масштабе mV, мм/мЧс-1. Соединив прямой точку Р'2 с центром вращения звена 3 получим прямую распределения линейных скоростей для точек звена 3, лежащих на линии центров. Угол, который образует эта прямой с линией центров, обозначим y3 . Угловые скорости звеньев определятся из этой схемы по формулам
Передаточное отношение, рассматриваемого рядного зубчатого механизма, будет равно
Формула Виллиса.
Формула Виллиса выводится на основании основной теоремы зацепления и устанавливает
соотношение между угловыми скоростями зубчатых колес в планетарном механизме.
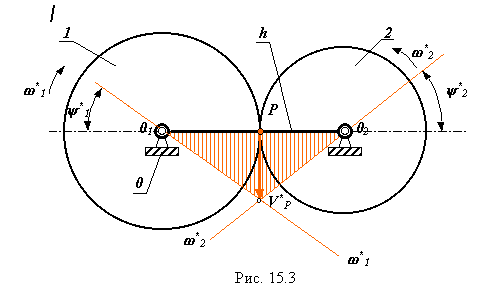
Рассмотрим простейший планетарный механизм с одним внешним зацеплением (см.
рис. 15.3). Число подвижностей в этом механизме равно
то
есть для получения определенности движения звеньев механизма необходимо сообщить
независимые движения двум его звеньям. Рассмотрим движение звеньев механизма
относительно стойки и относительно водила. Угловые скорости звеньев в каждом
из рассматриваемых движений приведены в таблице 15.2.
В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила. Если в движении относительно стойки ось зубчатого колеса 2 подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления.
Движение механизма относительно стойки
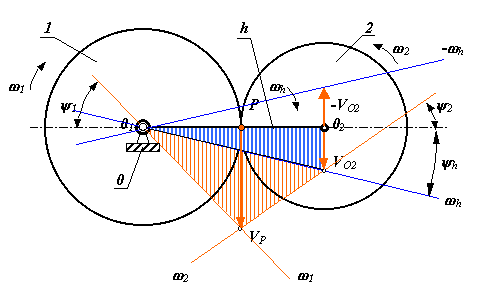
Движение механизма относительно водила
То есть можно записать выражение, которое называется формулой Виллиса для планетарных механизмов
Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами.
1. Двухрядный механизм с одним внутренним и одним внешним зацеплением.
Дано: Кинематическая схема механизма - ri , числа зубьев колес - zi ; _______________________________________________
Определить: Передаточное отношение механизма - ?
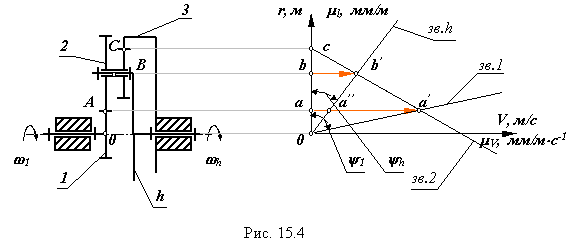
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис.15.4 на звене 2 нарезаны два зубчатых венца:
z2 , который зацепляется с зубчатым венцом z1 звена 1;
z3 , который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2 и z1
для внутреннего зацепления колес z4 и z3
Перемножим, правые и левые части этих уравнений, и получим
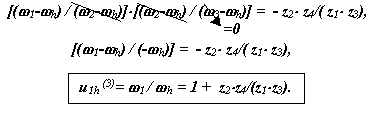
Графическое определение передаточного отношения.
В системе координат ri0V построим треугольники распределения линейных скоростей звеньев. Для этого из точки А с ординатой r1 в выбранном произвольном масштабе mV, мм/мЧс-1 отложим отрезок a a'. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на оси ri. Эта прямая образует с осью ri угол y1. Так как в точке с скорости звеньев 2 и 3 равны между собой и равны нулю, то соединяя точку с с прямой с точкой a', получим линию распределения скоростей для звена 2. Так как точка принадлежит звеньям 2 и h, то ее скорость определяется по лучу с a' для радиуса равного rB = (r1+r2), что в масштабе mV, мм/мЧс-1 соответствует отрезку bb'. Соединяя точку b' с началом координат прямой, найдем линию распределения скоростей для водила. Эта линия образует с осью ri угол yh. Передаточное отношение планетарного механизма определенное по данным графическим построениям можно записать так
2. Однорядный механизм с одним внутренним и одним внешним зацеплением.
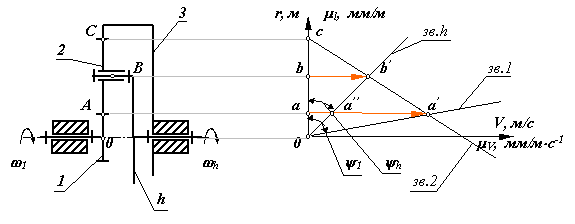
Аналитическое определение передаточного отношения.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2 и z1 :
для внутреннего зацепления колес z2 и z3:
Перемножим, правые и левые части этих уравнений, и получим:
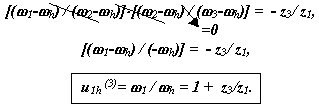
Графическое определение передаточного отношения.
3. Двухрядный механизм с двумя внешними зацеплениями.
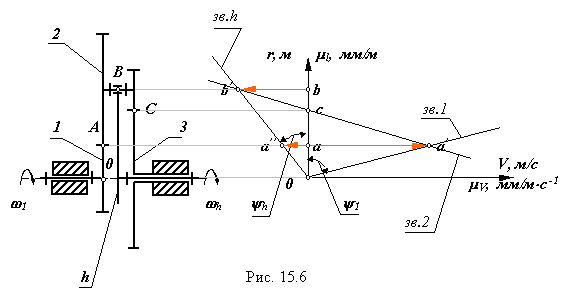
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис.15.6 на звене 2 нарезаны два зубчатых венца:
z2 , который зацепляется с зубчатым венцом z1 звена 1;
z3 , который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2 и z1 :
для внешнего зацепления колес z4 и z3:
Перемножим, правые и левые части этих уравнений, и получим:
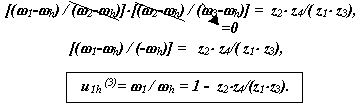
Графическое определение передаточного отношения.
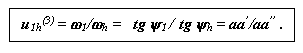
4. Двухрядный механизм с двумя внутренними зацеплениями.
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис.15.6 на звене 2 нарезаны два зубчатых венца:
z2 , который зацепляется с зубчатым венцом z1 звена 1
; z3 , который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев для внутреннего зацепления колес z2 и z1 :
для внутреннего зацепления колес z4 и z3:
Перемножим, правые и левые части этих уравнений, и получим:
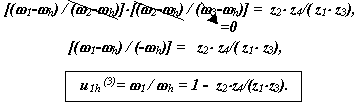
Графическое определение передаточного отношения.
Кинематическое исследование пространственных планетарных механизмов методом планов угловых скоростей.
Рассмотрим этот метод исследования на примере планетарного механизма конического дифференциала заднего моста автомобиля. На рис. 15.8 изображена схема механизма и планы угловых скоростей.
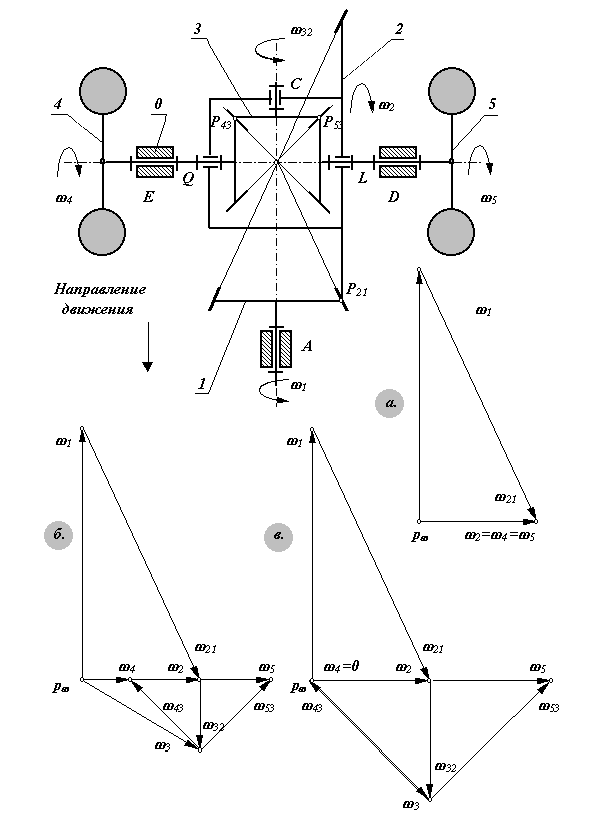
Планы угловых скоростей строятся в соответствии с векторными уравнениями:
|
w2=w1+w21; w4=w3+w43 |
w3=w2+w32; w5=w3+w53 |
Вектора относительных угловых скоростей направлены по осям мгновенного относительного вращения:
w21- по линии контакта начальных
конусов звеньев 2 и 1;
w32- по оси шарнира С;
w43- по линии контакта начальных конусов звеньев
4 и 3;
w53 - по линии контакта начальных конусов звеньев
5 и 3.
Вектора абсолютных угловых скоростей направлены по осям кинематических пар, которые образуют звенья со стойкой:
w2 - по оси пары В ;w1
- по оси пары А ;
w4 - по оси пары Е ; w5
- по оси пары D .
Направление угловой скорости сателлита 3 определяется соотношением величин угловых скоростей w2 и w32 .
Рассмотрим три режима движения автомобиля:
Для того, чтобы в условиях низкого сцепления колес с грунтом, уменьшить опасность их пробуксовывания в дифференциалы автомобилей высокой проходимости включают элементы трения или блокировки.
