| ЛЕКЦИЯ 18 |
|
Краткое содержание:
[Назначение и области применения]
[Преимущества
и недостатки волновых передач]
[Классификация типовых
структурных схем ВЗП]
[Структура волновой зубчатой
передачи]
[Кинематика волнового механизма]
[Расчет геометрии волнового зубчатого зацепления]
Волновые передачи:
Назначение и области применения:
Волновой передачей называется зубчатый или фрикционный механизм,
предназначенный для передачи и преобразования движения (обычно вращательного), в
котором движение преобразуется за счет волновой деформации венца гибкого колеса
специальным звеном (узлом) – генератором волн. Основными элементами
дифференциального волнового механизма являются: входной или быстроходный вал с
генератором волн, гибкое колесо с муфтой, соединяющей его с первым тихоходным
валом, жесткое колесо, соединенное со вторым тихоходным валом, корпус.
Рис. 18.1
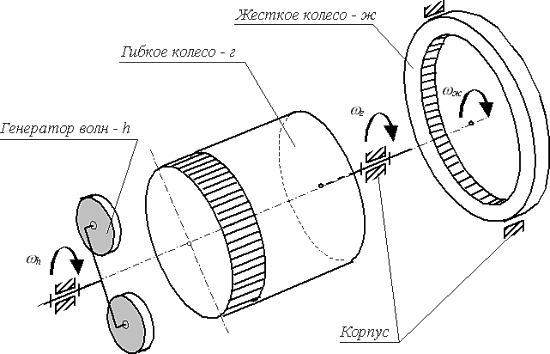
Существует большое количество конструкций волновых механизмов. Обычно эти механизмы преобразуют входное вращательное движение в выходное вращательное или поступательное. Волновые механизмы можно рассматривать как одну из разновидностей многопоточных планетарных механизмов, так как они обладают многозонным, а в случае зубчатого механизма, и многопарным контактом выходного звена с гибким колесом. Многозонный контакт обеспечивается за счет формы генератора волн (кулачок чаще с двумя, редко с тремя выступами), многопарный – за счет податливости зубчатого венца гибкого колеса. Такое сочетание позволяет волновым механизмам передавать значительные нагрузки при малых габаритах. Податливость зубчатого венца обеспечивает достаточно равномерное распределение нагрузки по зубьям, находящимся в зоне зацепления. При номинальных нагрузках процент зубьев находящихся в зацеплении составляет 15-25% от общего их числа. Поэтому в волновых передачах применяется мелкомодульное зацепление, а числа зубьев колес лежат в пределах от 100 до 600. Зона зацепления в волновой зубчатой передаче совпадает с вершиной волны деформации. По числу зон или волн передачи делятся на одноволновые, двухволновые и так далее. Передачи с числом волн более трех применяются редко. Распределение передаваемых усилий по нескольким зонам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный и многопарный контакт звеньев существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Поэтому волновые механизмы обладают высокой кинематической точностью и, несмотря на наличие гибкого элемента, достаточно высокой жесткостью. Образующиеся в структуре волнового механизма внутренние контуры, увеличивают теоретическое число избыточных или пассивных связей в механизме. Однако гибкое колесо за счет податливости компенсирует ряд возникающих перекосов. Поэтому при изготовлении и сборке волновых механизмов число необходимых компенсационных развязок меньше чем в аналогичных механизмах с жесткими звеньями.
Гибкое колесо обеспечивает волновым передачам возможность передачи движения через герметичную стенку, которая разделяет две среды (например, космический аппарат и открытый космос). При этом гибкое колесо выполняется как элемент герметичной стенки, входной вал и генератор волн располагаются по одну сторону стенки (внутри космического аппарата), а выходное звено – по другую (в космическом пространстве). Схема герметичной волновой передачи приведена на рис. 18.2.
Рис. 18.2
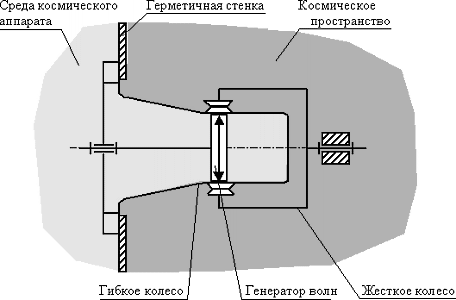
Преимущества и недостатки волновых передач:
Преимущества:
Структура волновой зубчатой передачи:
Рассмотрим одноволновую зубчатую передачу с генератором волн, который образует с гибким колесом пару скольжения. Волновая передача не может рассматриваться в рамках ранее принятых нами допущений, так как в ней содержится гибкое звено. Поэтому необходимо определить место гибкого элемента в структуре механизма. Гибкая связь обычно допускает по действием силовых воздействий определенные относительные перемещения соединяемых звеньев. Поэтому ее отнесем к отношениям между элементами или к упругой кинематической паре. Зубчатое колесо представляет собой замкнутую систему зубьев. В каждый рассматриваемый момент в контакте в высшей паре могут находится один или несколько зубьев. Так как зубчатые колеса – звенья, то зубья – элементы высшей кинематической пары. Поэтому многопарный контакт между зубчатыми колесами является контактом между элементами одной кинематической пары. Пассивные или избыточные связи, возникающие в этом контакте, относятся к внутренним связям кинематической пары и в структурном анализе на уровне звеньев не учитываются. Поэтому считаем, что в зацеплении находится один зуб. Структурная схема механизма с остановленным жестким колесом при гибком соединении зуба с валом гибкого колеса может быть представлена следующем образом.
|
Рис. 18.3 Волновая зубчатая передача с упругой муфтой – стаканом. 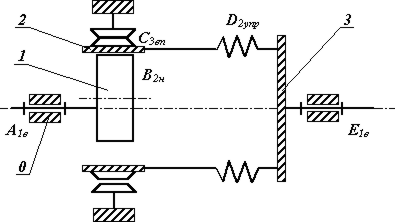 |
|
Рис. 18.4 Волновая зубчатая передача с волновой зубчатой муфтой. 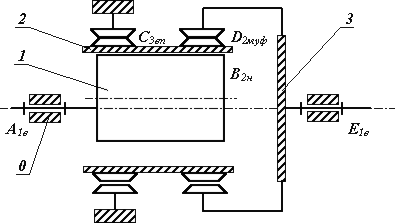 |
Рассмотрим звенья и кинематические пары механизмов:
|
|
|
|
|
|
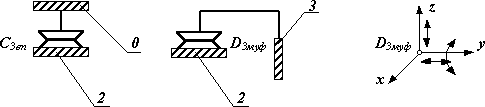
D3упр– двухподвижный упругий шарнир (рис.18.6). Данная кинематическая пара должна обеспечивать зубу гибкого колеса 2 возможность выполнять движения деформации относительно вала 3, но относительные движения в тангенциальном направлении (по оси х) запрещены. Аналогичные движения обеспечивает пара D3муф в зубчатом соединении в волновой зубчатой муфте и пара С3вп в волновом зубчатом зацеплении (рис.18.7).Оси координат в зубчатой паре направляются так:
ось z - по касательной к профилям в точке контакта, ось х – по нормали к профилям и ось у – по линии контакта зубьев.
Подвижность механизма подсчитывается следующим образом:
n = 3, p1 = 2, p2 = 1, p3 = 2.
Wпр = 6Ч 3 - 5Ч 2 - 4Ч 1 - 3Ч 2 = 18 – 20 = -2.
В механизме имеется одна местная подвижность
Wм= 1 – подвижность зуба гибкого
колеса в осевом направлении (по оси у).
Заданная или
основная подвижность механизма W0= 1.
Число избыточных связей в механизме равно:
qпр = W0 + Wм + Wпр = 1+1-
(-2) = 4.
Эти избыточные или пассивные связи определяют требование параллельности осей пар В,С,D и Е оси пары А.
Движение всех звеньев волнового механизма осуществляется в параллельных плоскостях. Поэтому механизм волновой зубчатой передачи можно рассматривать как плоский.
В этом случае:
n = 3; p1 = 3;
p2 = 2;
Wпл = 3Ч 3 - 2Ч 3 - 1Ч 2 = 9 – 8 = 1.
Wм= 0;
W0 = 1; qпл = W0 + Wм +
Wпл = 1-1 = 0.
Классификация типовых структурных схем ВЗП:
В таблице 18.1 приведены наиболее распространенные структурные схемы типовых волновых зубчатых передач, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях. Основное отличие одной схемы от другой заключается в конструкции муфты соединяющей гибкий зубчатый венец с корпусом или с выходным тихоходным валом. В таблице показаны только три наиболее распространенных разновидности: гибкая оболочка в форме стакана, гибкая труба с шлицевым соединением и волновая зубчатая муфта. Если в передаче с гибким колесом – кольцом (в третьей из рассматриваемых схем), второе волновое зацепление выполнить как волновую зубчатую передачу, то получим двухступечатую ВЗП.
Таблица 18.1
|
|
|
|
|
|
|
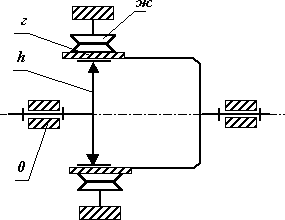 |
uh1ж= -zг / (zж- zг) |
|
|
|
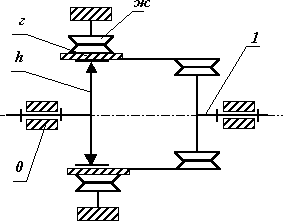 |
uh1ж= -zг / (zж- zг) |
|
|
|
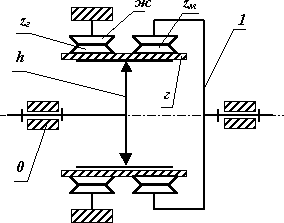 |
uh1ж = z1Чzг / |
|
|
Если zм= z1, то |
0.85..0.7 |
Кинематика волнового механизма:
Рассмотрим идеальную фрикционную волновую передачу. В этой передачи
контактирующие поверхности гибкого и жесткого колес будут соответствовать
начальным поверхностям зубчатых колес. Толщину гибкого колеса принимаем
бесконечно малой. Тогда срединная поверхность гибкого колеса совпадает с его
начальной поверхностью. Считаем, что срединная поверхность гибкого колеса
нерастяжима, то есть длина ее до и после деформирования колеса генератором волн
остается неизменной.
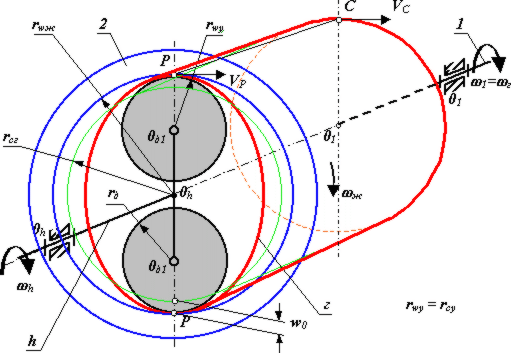
На рис.18.8 приняты следующие обозначения:
rwу - радиус начальной окружности условного колеса;
rwж - радиус начальной окружности жесткого колеса;
rд - радиус деформирующего диска;
rсг - радиус срединной окружности гибкого колеса;
rсу - радиус срединной окружности условного колеса;
w0 - радиальная деформация гибкого колеса.
Рассмотрим движение звеньев дифференциального волнового
механизма относительно генератора волн.
Тогда
угловые скорости звеньев изменятся следующим образом:
Таблица 18.2
| Движение механизма | Звено г | Звено ж | Звено h | Звено 0 |
| относительно стойки | wг | wж | wh | w0=0 |
| относительно генератора волн | w*г=wг-wh | w*ж=wж-wh | wh-wh=0 | -wh |
В движении звеньев относительно генератора волн скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость генератора. Скорость точки жесткого колеса, совпадающей с полюсом зацепления VPж = (wж- wh) Чrwж,а скорость точки, совпадающей с полюсом на гибком колесе VPг = (wг- wh) Чrwг
В полюсе зацепления нет скольжения и VPж = VPг, а так как срединную поверхность оболочки считаем нерастяжимой то VPг = VС . Тогда для движения относительно генератора волн
VPж = (wж- wh) Ч rwж ; VС = (wг- wh) Ч rwг
VPж = VС Ю (wж- wh) Ч rwж = (wг- wh) Ч rwг
(wж- wh)/ (wг- wh) =
rwг / rwж = zг / zж ,
| zж Ч wж + (zг – zж) Ч wh - zгЧ wг = 0. |
Для волнового зубчатого редуктора (1) :
| uhгж = wh / wг = - zг / (zж – zг) |
| uhжг = wh / wж = zж / (zж – zг) |
Расчет геометрии волнового зубчатого
зацепления:
В расчете геометрии волнового
зацепления существует два основных подхода. В первом методе (2)
исследуется относительное движение зубьев и, на основе этого, разрабатываются
рекомендации по выбору геометрических параметров зацепления. Второй метод
(3) основан на использовании расчетного внутреннего зацепления жесткого
колеса с условным расчетным колесом. Это колесо вписывается в деформированное
гибкое колесо на участке возможного зацепления. Преимуществом первого метода
можно считать относительную универсальность, которая позволяет в расчете
геометрии учитывать деформации как гибкого, так и жесткого колеса под нагрузкой.
Однако разработать рекомендации даже для небольшого количества конструкций ВЗП
затруднительно. Второй метод позволяет использовать для расчета геометрии
стандартный расчет внутреннего эвольвентного зацепления для пары колес
zжи
zу.
Число зубьев условного колеса рассчитывается по следующей
формуле:
| zy = zг / ( 1 ± kb Чmw) |
где:
mw= w0 / rсг - относительная деформация гибкого колеса.После определения zy определяются:
kb - коэффициент, определяемый углом b
b - угловая координата участка постоянной кривизны деформированной кривой гибкого колеса.
Литература: