Рассмотрим вариант метода с применением одномерной минимизации. На каждой итерации процедура осуществляет итеративный поиск вдоль n линейно независимых и ортогональный направлений. Когда получена новая точка в конце итерации, строится новое множество ортогональных векторов. На рисунке новые направления обозначены через q1 и q2.
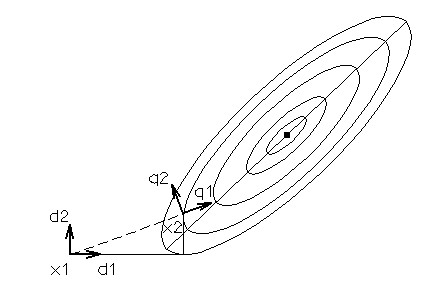
Построение новых направлений поиска в методе Розенброка.
Построение направлений поиска
Пусть d1,..., dn - линейно независимые векторы, по норме равные единицы. Предложим, что эти векторы взаимно ортогональны, т. е. (di*dj) = 0 для i != j. Начиная из текущей точки xk, целевая функция последовательно минимизируется вдоль каждого из направлений, в результате чего получается точка x[k+1]. В частности, x[k+1]- xk = Sum(lymj*dj), где lymj - длина шага по направлению dj. Новый набор направлений q1,..., qn строится с помощью процедуры Грамма-Шмидта следующим образом:
dj, если lym j = 0,
aj = {
Sum(lymi*di), i=[j,n], если lymj != 0,
aj, при j = 1,
bj = {
aj - Sum (aj*qi)*qi, i=[1,j-1], при j >= 2,
qj = bj /|| bj ||.
Новые направления построенные таким образом являются линейно независимыми и ортогональными.
Алгоритм метода Розенброка с минимизацией по направлению
Начальный этап. Пусть eps > 0 - скаляр, используемый в критерии остановки. Выбрать в качестве d1,..., dn координатные направления, начальную точку x1, положить y1= x1, k=j=1 и перейти к основному этапу.
Основной этап. Шаг 1. Найти lymj - оптимальное решение задачи минимизации f(yj+lymj*dj) при условии lym принадлежит E1 и положить y[j+1]= yj+lymj*dj. Если j < n, то заменить j на j+1 и вернуться к шагу 1. В противном случае перейти к шагу 2.
Шаг 2. Положить x[k+1]= y[n+1]. Если ||x[k+1] - xk|| < eps, то остановиться. В противном случае положить y1= x[k+1], заменить k на k+1 положить j=1 и перейти к шагу 3.
Шаг 3. Построить новое множество линейно независимых и взаимно ортогональных направлений в соответствии с процедурой Грамма-Шмидта. Обозначить новые направления d1,..., dn и вернуться к шагу 1.
