Цель занятия:практическое изучение алгоритмов объектно-ориентированной инвариантной обработки рекурсивных структур с использованием косвенной адресации компонент в абстрактном классе бинарных деревьев на примере унификации и систематизации потоков текстовых данных.

Формулировка задания:Требуется разработать программу-фильтр uni, которая унифицирует входной поток текстовых данных, исключая повторы строк, и упорядочивает оригинальные строки по алфавиту в выходном информационном потоке. Исходными данными программы uni является неограниченная последовательность символьных строк потока стандартного ввода (stdin).Результатом работы программы uni является лексиграфически упорядоченная последовательность оригинальных строк входного потока, которая должна отображаться через поток стандартного вывода (stdout). Для анализа повторений и перечисления уникальных входных строк в программе uni должны быть реализованы алгоритмы поиска по бинарным деревьям и систематического прохождения бинарных деревьев, соответственно. Программа uni должна быть составлена в системе программирования С++ с использованием косвенной адресации компонентных методов и описания виртуальных интерфейсов для реализации инвариантной обработки бинарных деревьев в абстрактных классах.

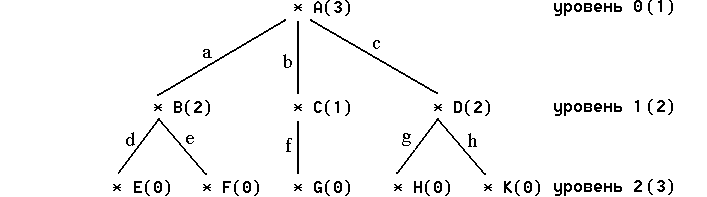
В теории графов конечное корневое дерево формально определяется как непустое конечное множество узлов Т, таких что: существует один, специально выделенный узел, называемый корнем, а остальные узлы образуют попарно непересекающиеся подмножества множества узлов Т, каждое из которых является деревом. Это определение позволяет интерпретировать корневое дерево как рекурсивный объект, который содержит сам себя и определяется с помощью себя самого (т. е. дерево определяется в терминах дерева). Определение корневого дерева как определение любого рекурсивного объекта содержит базисную и рекурсивную части. Базисная часть, определяющая корень дерева является нерекурсивным утверждением. Рекурсивная часть определения записана так, чтобы она редуцировалась (сводилась) к базе цепочкой повторных применений. В данном случае дерево с числом узлов n>1 индуктивно определяется через деревья с числом узлов меньше, чем n, пока не достигнут базисный шаг, где дерево состоит из единственного узла - корня. Рекурсивное определение корневого дерева позволяет более простым способом формализовать его структуру и алгоритмы обработки. Для неформального описания корневых деревьев часто используется генеалогическая терминология, согласно которой каждая ветвь отражает отношение потомок-предок между инцидентными ей узлами. Корень дерева- это узел, который не имеет предка.Узлы дерева, которые не имеют потомков называются листьями. Остальные узлы (не листья и не корень) называются разветвлениями. Следующий рисунок иллюстрирует классическое изображение корневого дерева средствами теории графов, где вершины и ребра графа представляют узлы и ветви дерева.

Рис. Изображение корневого дерева в теории графов .

На этом рисунке заглавные буквы латинского алфавита обозначают узлы, а строчные- ветви корневого дерева. Конфигурация ветвей этого корневого дерева такова, что узел А является корнем, узлы В С и D- разветвлениями, а узлы E, F, G, H, и K - листьями.
Следует отметить, что кроме классического изображения, принятого в теории графов, в области информационных технологий применяются альтернативные способы представления корневых деревьев. На следующем рисунке приведены 3 эквивалентных способа представления исходного корневого дерева: с помощью вложенных скобок (а), уступчатого списка (б) и десятичной системы Дьюи (в) соответственно:

Приведенные альтернативные способы представления корневых деревьев иллюстрируют возможности практического применения иерархических структур.
Например, десятичная система Дьюи применяется в библиографии, а вложенные скобки - для получения полноскобочной записи при грамматическом разборе арифметических выражений.
Важными метрическими характеристиками корневого дерева является степень и уровень узла. Степенью узла корневого дерева считается число поддеревьев, для которых он является корнем. Для рассмотренного примера корневого дерева: корень А имеет степень 3, степени разветвлений B и D - равны 2, а степень разветвления С равна 1. Степени остальных узлов равны 0, потому что они являются листьями, т. е. не имеют поддеревьев. Уровень узла корневого дерева определяется длиной пути, образованного чередующейся последовательностью узлов и ветвей, который соединяет его с корнем. Длина пути измеряется числом узлов в нем. Для рассмотренного примера корень А имеет уровень 1, разветвления   B, C и D имеют уровень 2, а листья E, F, G, H и K - уровень 3.
При измерении длины пути числом ветвей в нем, указанные уровни узлов надо уменьшить на 1.
Обобщением понятия корневого дерева является понятие леса. Под лесом понимается упорядоченное множество непересекающихся корневых деревьев. Отражением близости этих понятий является простота преобразований дерева в лес и наоборот, леса в дерево. Исключение корня превращает дерево в лес.
Наоборот, добавление одного узла превращает лес в дерево, где этот узел становится корнем. Чтобы подчеркнуть близость этих понятий, в некоторых работах для обозначения леса из N деревьев употребляют термин: дерево с N -кратным корнем.

Важной разновидностью корневых деревьев является класс бинарных деревьев, где каждый узел может иметь не более 2-х потомков. В рекурсивном варианте определения бинарное дерево состоит из корня и 2-х бинарных поддеревьев: левого и правого, причем любое из них может быть пустым. Следующий рисунок иллюстрирует изображение бинарного дерева из 8-ми узлов A, B, C, D, E, F, G, H средствами теории графов.

   Рис. Изображение бинарного дерева в теории графов.

Несмотря на иерархическую структуру бинарные деревья не являются подмножеством множества деревьев. Например на следующем рисунке показаны 2 различных бинарных дерева, которые эквивалентны как корневые деревья.

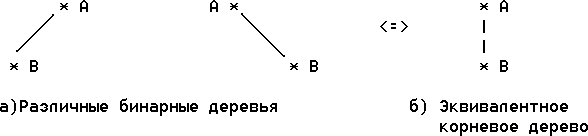
  Рис. Отличие корневых и бинарных деревьев
Эти бинарные деревья различны по структуре, потому что корень первого из них имеет только левый потомок, а корень второго - только правый. Однако, как деревья они эквивалентны дереву из 2-х узлов А и В, которое изображено на том же рисунке справа. В общем случае различие между корневым деревом и бинарным деревом состоит в том, что каждый узел корневого дерева может иметь произвольное число поддеревьев, в то время как любой узел бинарного дерева может иметь только 0, 1 или 2 поддерева и существует различие между левыми и правыми поддеревьями.
Несмотря на эти отличия бинарные деревья могут быть использованы для представления корневых деревьев. Возможность такого представления устанавливает следующее естественное соответствие между корневыми и бинарными деревьями. Левая ветвь каждого узла соединяет его с первым узлом следующего уровня, а правая - с другими узлами следующего уровня (братьями). Следующий рисунок демонстрирует естественное соответствие 3-х уровневого корневого дерева его бинарному представлению.

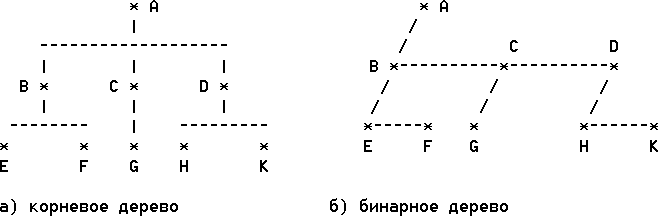
   Рис. Естественное соответствие между корневым и бинарным деревьями.

Естественное соответствие между корневыми и бинарными деревьями имеет важное значение в области информационных технологий, где программирование обработки данных может быть более просто реализовано для бинарных деревьев. Классическим примером иерархической обработки данных являются алгоритмы поиска по бинарному дереву и прохождения бинарного дерева в различном порядке.

Популярным приложением бинарных деревьев, например, в технологиях баз данных является поиск требуемых элементов во входном потоке информации. Наиболее быстрый поисковый алгоритм основан на использовании бинарного дерева поиска. Дерево поиска - бинарное дерево, узлы которого упорядочены по ключам, таким образом, что ключ левого потомка меньше ключа предка, а ключ правого потомка больше ключа предка. Указанное соотношение порядка иллюстрирует следующий фрагмент бинарного дерева поиска.

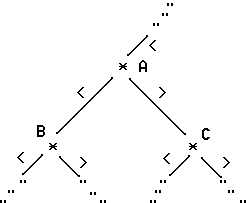
Рис.  Фрагмент бинарного дерева поиска.

В приведенном рисунке фрагмента бинарного дерева поиска ключ узла "В" меньше ключа узла "А", а ключ узла "С"больше ключа узла "А", т. е.
         key(B) < key(A)      и       key(C) > key(A)
Правило сравнения ключей определяется типом ключевых данных. Скалярные ( например, целочисленные) ключи упорядочиваются естественным образом по их величинам. Векторные ( например, символические) ключи упорядочиваются лексиграфически. Лексиграфический порядок образует упорядочивание векторов последовательно по величинам компонент.
Например. вектор V=(V1,..,Vj,..,Vp) лексиграфически больше, чем вектор W=(W1,..,Wj,..,Vp), если Vj=Wj при j<q и Vq>Wq.
Место очередного элемента в бинарном дереве поиска определяется путем сравнения его ключа с ключами существующих узлов, начиная с корня. В зависимости от результата каждого сравнения ключей, для продолжения поиска выбирается либо левое, либо правое поддерево текущего узла, если его ключ не равен ключу искомого образца. Поиск считается успешно завершенным, когда найден узел, ключ которого равен ключу искомого элемента. В противном случае, когда достигнут лист и нет соответствия образцу по ключу, необходимо расширить дерево поиска, добавив новый узел, либо в правую, либо в левую ветвь листа в зависимости от соотношения ключей. Методическая необходимость добавления новых узлов позволяет более строго называть рассмотренный алгоритм поиском по бинарному дереву со вставкой. Приведенное описание следует рассматривать как неформальное изложение данного алгоритма. Ниже рассмотрен классический пример поиска по бинарному дереву знаков зодиака.

На следующем рисунке изображено бинарное дерево поиска знаков зодиака, которое содержит 11 узлов с символическими векторными ключами, соответствующими латинским названиям знаков зодиака.

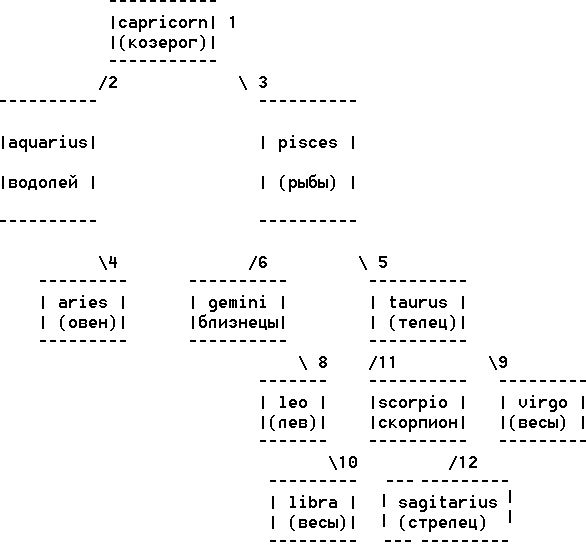
Это бинарное дерево построено последовательной вставкой новых узлов в следующем порядке: capricorn, aquarius, pisces, aries, taurus, gemini, cancer, leo, virgo, libra, scorpio, начиная с корня. Поиск существующего в дереве знака libra (весы) образует следующую последовательность сравнения ключей:
        libra > capricorn  - поиск в правом поддереве capricorn;
        libra < pisces     - поиск в левом поддереве pisces;
        libra > gemini     - поиск в правом поддереве gemini;
        libra > leo        - поиск в правом поддереве leo;
        libra = libra      - поиск завершен успешно.
Поиск отсутствующего в дереве знака sagittarius (стрелец) образует следующая последовательность сравнения ключей:

        sagittarius > capricirn - поиск в правом поддереве capricorn;
 sagittarius > pisces    - поиск в правом поддереве pisces;
 sagittarius < taurus    - поиск в левом поддереве taurus;
 sagittarius < scorpio   - поиск в левом поддереве scorpio;
Поскольку левое поддерево узла scorpio пусто, то для завершения поиска нужно добавить новый узел sagittaruis, который показан пунктиром на рисунке. Следует отметить, что если для поиска в бинарном дереве знаков зодиака использовать скалярные ключи, например, порядковые номера или диапазоны дат соответствующих знаков, то структура бинарного дерева и траектория поиска были бы иными , чем в рассмотренном варианте векторных ключей. Также другой результат был бы получен, если для ключей применить русские названия знаков зодиака, которые указаны на рисунке для перевода соответствующих латинских обозначений.

Прохождение (или обход) бинарного дерева означает систематическое перечисление всех узлов для выполнения необходимой функциональной обработки. Наиболее известны и практически важны 3 способа прохождения, которые отличаются порядком и направлением обхода бинарного дерева. Можно проходить узлы в прямом порядке (сверху-вниз), в симметричном порядке (слева-направо) и, наконец, в концевом порядке (снизу-вверх).
Рекурсивные алгоритмы прохождения бинарного дерева по каждому из перечисленных способов включают 3 одинаковых процедуры, где нужно пройти корень поддерева, левое поддерево текущего корня и правое поддерево текущего корня. Направление обхода однозначно определяет последовательность выполнения указанных процедур. Последовательность их рекурсивного вызова для каждого способа прохождения перечислена в следующей таблице.

 Таблица рекурсивных алгоритмов прохождения бинарного дерева.
----------------------------------------------------------------------------------
                           Порядок прохождения
----------------------------------------------------------------------------------
        Прямой                  |     Симметричный         |       Концевой
-----------------------------------------------------------------------------------
1. Корень поддерева     |1. Левое поддерево        |1. Левое поддерево
2. Левое поддерево       |2. Корень поддерева      |2. Правое поддерево
3. Правое поддерево     |3. Правое поддерево      |3. Корень поддерева
-----------------------------------------------------------------------------------

Прямой порядок прохождения означает обход в направлении сверху-вниз, когда после посещения очередного разветвления продолжается прохождение вглубь дерева, пока не пройдены все потомки достигнутого узла. По этой причине прямой порядок прохождения часто называют нисходящим, или прохождением в глубину. Прямой порядок есть наиболее естественный способ перечисления узлов дерева в форме вложенных скобок или уступчатого списка. Если исключить все скобки и запятые, то последовательность узлов в форме вложенных скобок будет соответствовать прямому порядку прохождения дерева. Уступы в ступенчатом списке, представляющем любую иерархическую структуру, также располагаются в прямом порядке. В генеалогических терминах прямой порядок прохождения дерева отражает династический порядок престолонаследования, когда титул передается старшему потомку. При симметричном порядке дерево проходится слева-направо, порождая лексиграфически упорядоченную последовательность ключей узлов. По этой причине симметричный порядок прохождения часто называют лексиграфическим. В частности, такой способ прохождения бинарного дерева знаков зодиака располагает их названия в лексиграфическом порядке:

  aquarius < aries < canser < capricorn < gemini < leo < ... < virgo

следует отметить, что симметричность порядка выражается в том, что если бинарное дерево отразить относительно вертикальной оси, поменяв местами левые и правые узлы, то симметричный порядок прохождения заменится на противоположный лексиграфический.
Если применяется концевой порядок прохождения, то получается обход дерева снизу-вверх, когда в момент посещения любого узла все его потомки уже пройдены, а корень дерева проходится последним. Из-за этой особенности обхода, концевой порядок часто называют восходящим, или обратным относительно прямого.
При выборе определенного порядка прохождения требуемая функциональная обработка каждого узла происходит после соответствующего числа заходов в него. При обходе сверху-вниз каждый узел обрабатывается при первичном заходе в него, при симметричном порядке прохождения - во втором, а при обходе снизу-вверх - в третьем. Рассмотренные варианты прохождения иллюстрирует траектория обхода бинарного дерева, изображенного на следующем рисунке.

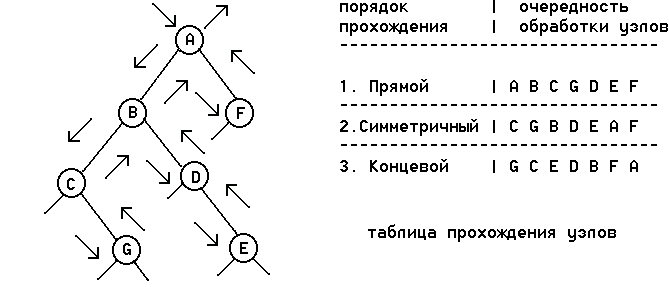
Рис. Траектория обхода бинарного дерева.

На этом рисунке стрелками обозначена траектория обхода бинарного дерева. Последовательности обработки узлов для бинарного дерева рассматриваемого примера при различных порядках прохождения сведены в таблицу на том же рисунке. По сложившейся традиции процедуры прохождения бинарного дерева в прямом, симметричном и концевом порядке принято называть PREORDER, INORDER и POSTORDER, соответственно, учитывая их применение для прохождения семантических деревьев, которые строятся для грамматического разбора арифметических выражений. Прохождение семантического дерева грамматического разбора в прямом, симметричном и концевом порядке представляет арифметическое выражение соответственно в префиксной, инфиксной и постфиксной форме. Независимо от конкретного приложения наиболее естественными являются рекурсивные варианты процедур прохождения бинарных деревьев, поскольку они как деревья относятся к классу объектов с рекурсивно определенной структурой. Как известно, процедура называется рекурсивной, если она явно или неявно, вызывает сама себя, порождая соответствующее число независимых последовательных активаций. При этом выполнение каждой предшествующей активации ожидает завершение последующей активации в той точке процедуры откуда она "самовызвана". Таким образом выполняется всегда только последняя активация, причем в контексте своих предшественников, которые находятся в состоянии ожидания завершения своих потомков.
Рекурсивные процедуры прохождения бинарных деревьев в различном порядке имеют сходную прямо-рекурсивную структуру, которая предусматривает явное обращение каждой из них к себе самой для левого и правого потомка текущего узла, а также обеспечивает нерекурсивную обработку текущего узла.  Например, псевдокод процедуры INORDER для прохождения бинарного дерева в симметричном порядке содержит следующие операторы:

  IF THIS <> NULL THEN
  {
  INORDER (LEFT); /*рекурсия для левого потомка*/
  VISIT (THIS);   /*нерекурсивная обработка     */
  INORDER (RIGHT) /*рекурсия для правого потомка*/
  {
  RETURN;

Где THIS используется для ссылки на текущий узел дерева, LEFT и RIGHT - для идентификации левого и правого потомков текущего узла, а VISIT (THIS) обозначает процедуру функциональной обработки текущего узла.
При начальном обращении к процедуре INORDER ее аргумент должен идентифицировать корень бинарного дерева (root). Последующие рекурсивные вызовы порождают активации процедуры INORDER для различных потомков корня с целью прохождения бинарного дерева в требуемом симметричном порядке.
Важное преимущество рекурсивных алгоритмов по сравнению с традиционными итерационными - простота и выразительность вычислительной схемы. Чисто алгоритмически рекурсия всегда может быть использована вместо итерации для организации повторяющихся действий. С другой стороны рекурсия не всегда заменяется итерацией. Поэтому пока рекурсия доступна и эффективна, рекурсивные управляющие структуры более предпочтительны, чем их итерационные аналоги, особенно для обработки данных, структура которых определена рекурсивно.
Практическая эффективность использования рекурсии вместо итерации обусловлена возможностями программной реализации. При программной реализации эффективность рекурсии ограничена ресурсными сообщениями, которые связаны с необходимостью хранения во внутреннем стеке программы последовательности активаций вместе с необходимыми им значениями локальных переменных и аргументов рекурсивной процедуры. Поскольку размер внутреннего стека ограничен, то глубина рекурсии не может быть произвольной. Таким образом, если ожидается обработка значительных информационных массивов, когда ресурсные требования рекурсивной процедуры могут превысить размер программного стека то следует отдать предпочтение нерекурсивной версии алгоритма, как более эффективной и безопасной. Аналогичный выбор рекомендуется сделать, когда трудоемкость понимания рекурсивного и итерационного вариантов примерно равны.
Для сравнения, ниже приводится итерационный вариант процедуры INORDER прохождения бинарного дерева в симметричном порядке, где применяется собственный внешний стек вместо внутреннего стека в адресном пространстве программы рекурсивной процедуры. Псевдокод итерационной процедуры прохождения бинарного дерева в симметричном порядке образует следующие операторы:

  S <= (ROOT,1)
  WHILE S <> 0
  {
  (THIS,i) <= S;
  CASE i = 1 : S <= (THIS,2); VISIT (THIS)
  CASE i = 2 : S <= (THIS,3);
        IF LEFT <> NULL THEN S <= (LEFT,1);
  CASE i = 3 : IF RIGHT <> NULL THEN S <= (RIGHT,1);
  }
  RETURN;

В этом алгоритме дополнительно к обозначениям рекурсивного варианта вводится собственный стек S для хранения пар, состоящих из ссылки на текущий узел дерева THIS и целочисленной переменной i. Ее значение указывает, какую из 3-х операций прохождения нужно применить к текущему узлу, когда пара достигнет вершины стека и будет извлечена для обработки. Итерационные варианты 2-х других процедур прохождения бинарного дерева конструируются по сходной схеме. Необходимый объем памяти для внешнего стека в них может динамически распределяться из кучи или принадлежать сегменту данных из адресного пространства программы итерационной процедуры. В любом случае внешний стек итерационной процедуры менее чувствителен к ограничениям операционной среды, чем внутренний стек ее рекурсивного варианта. С другой стороны сравнительная оценка сложности обоих аналогов процедуры INORDER однозначно в пользу рекурсивного алгоритма.

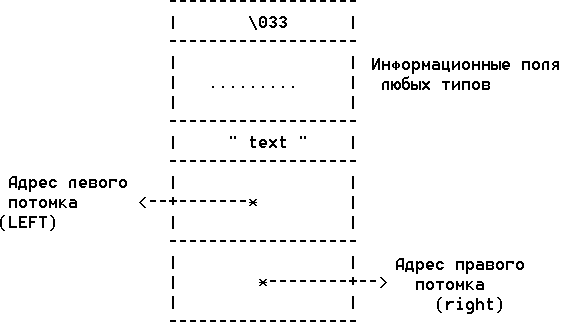
Для программной реализации бинарных деревьев чаще всего используют динамические структуры данных, в которых каждый узел управляется записью из 2-х адресных и требуемого числа информационных полей. Адресные поля узла предназначены для хранения адресов левого и правого потомков. При отсутствии левого или правого потомка соответствующим адресным полям узла можно присвоить нулевые значения (NULL). Адресные поля имеют тип указатель на узел бинарного дерева. Информационные поля узлов могут иметь произвольный тип. Они используются для хранения данных и ключей в узлах бинарного дерева. Диаграмма логической структуры узла бинарного дерева представлена на следующем рисунке.

При создании нового узла бинарного дерева в динамической реализации, из кучи распределяется область памяти, объем которой необходим для хранения всех полей его логической структуры. Адрес области памяти, выделенной для нового узла, сохраняется в соответствующем (левом или правом) адресном поле предка.
Динамическое распределение узлов по адресным полям предков позволяет конструировать бинарные деревья с желаемой иерархической структурой информационных полей.
Например, на следующем рисунке приведена логическая структура динамической реализации семантического дерева грамматического разбора арифметического выражения: 7+6*4 .

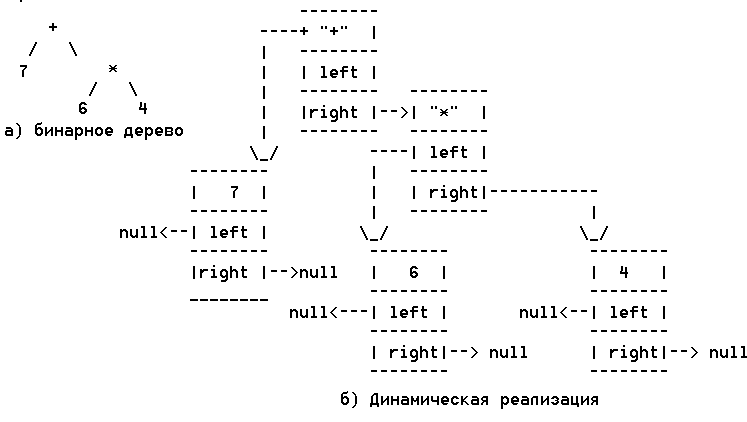
Рис. Логическая структура бинарного дерева

Требуемый по заданию процесс обработки символьных строк программой UNI можно алгоритмически разделить на 2 этапа: унификация входных данных и систематизированное представление результатов.
Унификация данных на этапе 1 означает исключение дубликатов символьных строк, поступающих из потока стандартного ввода (STDIN). Она обеспечена поиском по бинарному дереву, который исключает повторы входных строк, но сохраняет оригиналы в логической структуре бинарного дерева. Поскольку входные строки должны поступать из потока стандартного ввода, то для их чтения рекомендуется применять стандартную библиотечную функцию GETS систему программирования С и С++,  зарезервировав статический символьный буфер для получения каждой очередной строки. Емкость буфера должна превышать размер самой длинной ожидаемой строки. Параллельно процессу чтения входных строк, на этапе 1 должно строится бинарное дерево, информационные поля узлов которого сохраняют оригинальные строки из потока стандартного ввода. Адресные поля узлов бинарного дерева должны обеспечивать иерархию поиска очередной входной строки для проверки ее уникальности. Ввод уникальных строк будет динамически развивать бинарное дерево поиска путем добавления новых листьев. Ввод дубликатов не должен приводить к модификации бинарного дерева, но должен фиксироваться соответствующим предупреждением в потоке стандартной диагностики (STDERR). Ввод первой строки должен форсированно приводить к формированию корня бинарного дерева без проверки ее уникальности. Адрес корня следует сохранить в отдельной переменной (ROOT) для доступа к остальным узлам бинарного дерева, вырастающего из данного корня. Рекомендуется распределение корня выполнить отдельно, до цикла обработки остальных строк. Циклическая процедура унификации входного потока символьных строк должна продолжаться пока не исчерпан поток стандартного ввода. Признаком конца потока стандартного ввода следует считать нулевой возврат (NULL) функции GETS. Завершение ввода входных строк означает окончание этапа 1 и автоматический переход к этапу 2.
На этапе 2 должно осуществляться систематизированное представление результатов унификации входных строк по бинарному дереву этапа 1. Это означает перечисление входных строк в алфавитном порядке. Достижение указанной цели обеспечивает прохождение бинарного дерева этапа 1 в симметричном порядке. Упорядоченный по алфавиту список входных строк должен отображаться через поток стандартного вывода (STDOUT). После завершения указанной обработки необходимо ликвидировать бинарное дерево, корректно освободив память, которая была динамически распределена под его узлы на этапе 1. Для очистки памяти рекомендуется использовать процедуру прохождения бинарного дерева в концевом порядке (снизу-вверх), последовательно исключая все узлы в направлении от листьев к корню.
Следует отметить, что характер информационной обработки узлов на этапе 2 не зависит от порядка прохождения бинарного дерева. Например, удаление бинарного дерева могло быть реализовано при любом порядке обхода узлов, а печать информационных полей могла сопровождаться нумерацией, шифрацией, дешифрацией и т. п. Аналогично, более привлекательной выглядит инвариантная структура процедура поиска на этапе 1, которая не зависит от типа ключевых информационных полей узлов, и обеспечивает универсальный поиск по ключам любого типа (целочисленным, символическим и т. д.).
Указанная мобильность процедур прохождения и поиска по бинарному дереву достигается объектно-ориентированной обработкой данных на основе использования виртуальных интерфейсов и косвенной адресацией компонентных методов в базовом и производном классах бинарных деревьев.

Для объектно-ориентированной программной обработки бинарных деревьев целесообразно сконструировать базовый класс BiNode с защищенными компонентными данными и общедоступными компонентными методами. Компонентные данные класса BiNode следует использовать для формального описания узлов абстрактного бинарного дерева, в котором узлы имеют только адресные поля для связи с другими узлами, но не имеют каких-либо информационных полей.
Общедоступная часть класса BiNode должна включать инвариантные компонентные методы прохождения и поиска по бинарным деревьям, которые не зависят от информационной природы узлов.
Класс BiNode не должен быть предназначен для самостоятельного применения, т. к. узлы дерева без информационных полей не имеют смысла, потому что нельзя никак идентифицировать, что они найдены или пройдены. По этой причине, класс BiNode следует рассматривать как абстрактный класс, который не может быть реализован в объектах. Его следует применять только как базовый класс, который своими адресными полями обеспечивает поддержку иерархической структуры бинарного дерева производных узлов с любыми информационными полями и предоставляет инвариантные базовые методы древовидной обработки данных.
В терминах системы программирования С++ логическая структура декларации базового класса BiNode должна иметь следующий формат:

  class BiNode
  {
  protected:  /*спецификация компонентных данных*/
  public:     /*спецификация компонентных методов*/
  };

В защищенной (protected) части декларации класса BiNode рекомендуется специфицировать адресную пару компонентных данных:

  BiNode * left;  /*адрес левого потомка*/
  BiNode * right; /*адрес правого потомка*/

Для хранения адресов потомков каждого узла бинарного дерева или нулевых (NULL) указателей, при отсутствии соответствующих потомков. Для инициализации этих адресов нулевыми значениями в классе BiNode рекомендуется предусмотреть и явно описать собственный конструктор без аргументов, который удобно специфицировать как inline-подстановку непосредственно в декларации класса.
В общедоступную (public) часть объявления класса BiNode нужно включить декларацию универсальных базовых компонентных методов, которые программно реализуют алгоритмы прохождения (preorder,inorder и postorder) и поиска по бинарному дереву (search). Эти компонентные методы должны предусматривать инвариантный доступ к узлам бинарных деревьев из объектов различных производных классов, который не зависит от специфики обработки их информационных полей.
Компонентные методы preorder, inorder и postorder должны обеспечивать программную реализацию рекурсивных процедур прохождения бинарного дерева, соответственно в прямом, симметричном и концевом порядке. Их спецификация не должна зависеть то способов обработки данных при посещении узла. Например, обход бинарного дерева может проводится в следующих различных целях: отображение информационных полей узлов в заданном порядке, определение метрических характеристик бинарного дерева (уровни и степени узлов), представление бинарного дерева в желаемом формате (уступчатый список, вложенные скобки, десятичная система Дьюи), очистка памяти, динамически распределенной под узлы бинарного дерева. Перечисленные методы функциональной обработки при обходе узлов бинарного дерева могут быть реализованы в различных производных классах базового класса BiNode, для которых они актуальны. Универсальный интерфейс с различными методами функциональной обработки производных классов в инвариантных методах прохождения бинарного дерева может обеспечить косвенная адресация компонент, основанная на обращении к методу по его адресу в структуре его класса. По этой причине аргументы компонентных методов прохождения бинарного дерева должны обеспечивать передачу указателя на компонентный метод любого производного класса, обеспечивающий требуемую функциональную обработку при обходе. Поскольку имена производных классов при проектировании базового класса неизвестны, то указатели на методы функциональной обработки из них следует объявить как указатели на компонентные методы базового класса BiNode. По ним можно передавать указатели на компонентные методы производных классов при соответствующем явном преобразовании типов аргументов. Если ограничиться косвенной адресацией компонентных методов, которые не имеют возврата и аргументов (void), то для удобства спецификации аргументов методов прохождения бинарного дерева целесообразно ввести специальный тип VISIT, который должен определяться директивой typedef перед объявлением класса BiNode следующим образом:

  class BiNode;   /*декларация имени класса*/
  typedef void (BiNode::*VISIT) (void);
  class BiNode { /*спецификация класса*/ };

Директива typedef в данном случае определяет новый тип VISIT как указатель на компонентный метод класса BiNode (BiNode::*), у которого нет аргументов (void) и отсутствует код возврата (левый void в спецификации typedef). С учетом типа VISIT описание прототипа, например, компонентного метода inorder имеет следующий простой формат в декларации базового класса Binode:

 class BiNode {
  .............
  void inorder (VISIT): /*traversal by infix order*/
  .............
  };

Для вызова компонентного метода по его адресу в структуре класса, система программирования С++ предоставляет операторы разыменования (->*) или (.*) в зависимости от способа определения объекта класса (по указателю или по ссылке). При наличии типа VISIT вызов по адресу требуемого метода информационной обработки узлов для обхода бинарного дерева, например, в выше декларированном методе inorder, специфицируется с помощью оператора разыменования (->*) следующим образом:

  void BiNode
  {
  ...............
  (this ->* V) ();
  ...............
  }

Декларация и спецификация 2-х других компонентных методов прохождения бинарного дерева (preorder и postorder) может быть дана аналогично.
Компонентный метод search предназначается для реализации алгоритма поиска по бинарному дереву в соответствии с заданным ключом, который следует передавать ему как аргумент. Компонентный метод search должен возвращать адрес узла бинарного дерева, который соответствует ключу, или нулевой указатель (NULL), если объект с заданным ключом не был обнаружен при поиске.
По этой причине естественным типом кода возврата компонентного метода search является указатель на базовый класс (BiNode*). Передача ключа поиска должна быть организована по адресу. С этой целью у компонентного метода search следует предусмотреть аргумент типа (void*). Выбор такого типа аргумента обеспечит его независимость от типа данных ключа поиска, потому что по указателю типа (void*) можно передать адрес данных любого типа, например, адрес строки символов (char*), если требуется организовать поиск по символическому ключу.
С учетом обозначенных предпочтений по типу аргумента и кода возврата, компонентный метод search может быть декларирован в объявлении класса BiNode следующим образом:
  class BiNode
  {
  ...................
  BiNode* search (void*);
  };
Основными элементами спецификации компонентного метода search должны быть: организация направленного перебора существующих узлов бинарного дерева для идентификации по заданному ключу поиска и вставка нового узла, когда ключевой образец поиска не обнаружен. Обеспечивая внешнюю независимость компонентного метода search от типа данных ключа ( с помощью аргумента типа void*), необходимо также выбрать для него инвариантную внутреннюю структуру, которая не зависит от специфики идентификации ключа и вставки нового узла при поиске по бинарному дереву построенному из объектов любого производного класса. Желаемая инвариантность метода search может быть достигнута путем декларации в базовом классе BiNode виртуальных интерфейсов identify и insert, реализация которых планируется в производных классах. Базовый класс только объявляет виртуальные интерфейсы, устанавливая договоренность по типу аргумента и коду возврата.
В системе программирования С++ виртуальные интерфейсы декларируются как чистые (PURE) виртуальные функции, которые определяются в базовом классе как компонентные методы без исполняемого кода (имеют нулевой код). Не имея кода, чистые виртуальные функции не обладают реализацией в базовом классе. Чтобы приобрести код они перегружаются одноименными компонентными методами производных классов с соответствующими по типу аргументами и кодом возврата, получая специфичную реализацию в каждом производном классе. Несмотря на различие реализации в каждом производном классе, чистые виртуальные функции обладают идентичным интерфейсом, который установлен и декларирован базовым классом. Таким образом, упомянутые выше виртуальные интерфейсы identify и insert, декларируются в базовом классе BiNode соответствующими чистыми виртуальными функциями, которые определяются в производных классах.
Чистая виртуальная функция identify должна применятся в компонентном методе search, чтобы обозначить необходимость идентификации узлов бинарного дерева по заданному ключу поиска, который был передан методу search через аргумент типа (void*). Она должна обеспечивать целочисленный (int) код возврата и принимать ключевые данные по адресу через свой единственный аргумент, который должен иметь тип (void*) по соображениям, указанным выше. Код возврата используется для анализа результата сравнения заданного ключа поиска с ключевым информационным полем текущего узла бинарного дерева, для идентификации которого была вызвана виртуальная функция identify. Анализ результата идентификации ключа по текущему узлу следует использовать либо для завершения поиска, либо для его продолжения в левом или правом поддереве текущего узла в зависимости от знака кода возврата виртуальной функции identify. Рекомендуется принять следующую договоренность по знаку кода возврата при оценке результатов идентификации узла: нулевой код возврата означает соответствие текущего узла заданному ключу поиска, ненулевой - отсутствие соответствия, причем поиск следует продолжать в правом поддереве текущего узла, если код возврата больше нуля, либо в левом, когда код возврата виртуальной функции identify меньше нуля. Способ сравнения ключей определяется типом ключевых данных и реализуется особенным образом в каждом производном классе в соответствии с установленным интерфейсом базового класса BiNode.
Вторая чистая виртуальная функция insert, декларированная в базовом классе BiNode, используется в компонентном методе search, чтобы обозначить необходимость вставки нового узла в бинарное дерево, если в нем отсутствует узел, который соответствует ключу поиска. Она должна возвращать адрес нового узла бинарного дерева, принимая адрес ключа поиска, переданный в компонентный метод search через аргумент типа (void*). Это означает, что по типу кода возврата и типу аргумента виртуальная функция insert аналогична компонентному методу search, где она должна вызываться. Полученный от виртуальной функции insert адрес нового узла, который создается в ней, следует присвоить свободному адресному полю (left или right) идентифицированного узла в соответствии с текущим знаком ненулевого кода возврата виртуальной функции identify. Очевидно, что виртуальная функция insert может быть вызвана для идентифицированных узлов со степенью меньше чем 2 и только тогда, когда результат сравнения ключей требует продолжить поиск для поддерева, корнем которого должен являться отсутствующий потомок данного узла. Особенности реализации нового узла бинарного дерева   специфичны для каждого производного класса, т. к. зависят от структуры его информационных полей, и должны быть конкретизированы в производном классе. Эти особенности не являются существенными для базового компонентного метода search, кроме того, что вставка нового узла должна происходить в соответствии с интерфейсом базового класса.
Приведенное описание виртуальных интерфейсов базового класса, которые необходимы для реализации инвариантного поиска по бинарному дереву, отражает следующая декларация чистых виртуальных функций в классе BiNode:

  class BiNode
  {
  ...................
  virtual int identify (void*) = 0;
  virtual BiNode* insert (void*) = 0;
  ...................
  };

При обращении к чистой виртуальной функции базового класса выбирается подходящая реализация из производного класса, соответствующего по типу объекту, который инициирует ее вызов. В частности, вызовы компонентного метода search через указатели на объекты различных производных классов будут порождать вызовы различных производных реализаций чистых виртуальных функций identify и insert при обращении к ним через неявно передаваемый указатель this, который при такой схеме обращения сохраняет адрес объекта производного класса. Обращение к чистым виртуальным функциям через адрес объекта базового класса не имеет смысла из-за отсутствия их реализации в нем.
Следует отметить , что в соответствии с терминологией системы программирования С++ класс BiNode является абстрактным классом. По правилам системы программирования С++ абстрактным называется класс, который содержит хотя бы 1 чистую виртуальную функцию (Базовый класс BiNode объявляет сразу 2 чистые виртуальные функции.). Абстрактный класс не может быть реализован в объекте, но указатели или ссылки на него вполне допустимы. Производные классы, где перегружены унаследованные от базового класса чистые виртуальные функции, абстрактными не являются и, следовательно, могут быть реализованы в объектах. Существует мнение, что абстрактные классы особенно полезны для программирования иерархических структур. В данном случае абстрактный класс BiNode определяет универсальную структуру и методы обработки бинарных деревьев, узлы которых могут быть реализованы объектами любых производных классов.

Чтобы учесть специфику иерархической обработки для унификации и систематизации символьных строк в программе uni, целесообразно сформировать класс StrNode, производный от базового класса бинарных деревьев BiNode. Объекты класса StrNode должны описывать иерархию бинарного дерева, узлы которого предназначены для хранения текстовых строк. Производный класс StrNode должен наследовать компоненты базового класса и содержать собственные частные (private) компоненты-данные и общедоступные (public) компонентные методы, учитывающие особенности иерархической обработки символьных строк. В соответствии с правилами реализации принципа наследования в системе программирования С++, декларацию класса StrNode можно специфицировать следующим образом:

  class StrNode : public BiNode
  {
  private : /*спецификация собственных компонент-данных*/
  public  : /*спецификация собственных компонентных методов*/
  };

Категория наследования public выбрана для того, чтобы сохранить в производном классе привилегии доступа к компонентам, установленные в базовом классе.
В спецификацию собственных частных компонент производного класса StrNode следует включить объявление информационного поля str типа (char*) для хранения адресов строк текстовых данных. Содержание поля str одновременно используется для идентификации узла по ключу в алгоритме поиска по бинарному дереву, выращенному из производных объектов класса StrNodE, а также для выполнения информационной обработки при обходе узлов бинарного дерева.
Символьный тип информационных данных определяет особенности узлов бинарного   дерева производных объектов в классе StrNode и, соответственно, специфику их обработки.
Для инициализации текстовых данных при создании нового узла в классе StrNode рекомендуется предусмотреть конструктор с аргументом типа (char*), через который должно передаваться требуемое содержание поля str. Необходимый объем памяти для хранения переданных данных должен динамически выделяться из кучи с помощью оператора new системы программирования C++. Для оценки размера переданных данных и копирования их по адресу str рекомендуется использовать библиотечные функции strlen и strcpy, которые наиболее часто применяются для обработки символьных строк в системе программирования С. Для инициализации наследованных адресных полей базового класса BiNode, конструктор производного класса StrNode должен предусматривать вызов конструктора базового класса без аргументов BiNode(). Вызов конструктора базового класса следует обозначить в списке инициализаций конструктора производного класса, оформив заголовок его спецификации следующим образом:

  StrNode :: StrNode (char*s) : BiNode() {......}

Для очистки памяти, динамически распределенной конструктором, в классе StrNode следует предусмотреть деструктор ~StrNode(), который будет автоматически вызываться при удалении объектов данного класса. Для освобождения памяти, динамически распределенной по адресу str, деструктор класса StrNode должен использовать оператор delete системы программирования С++. Рекомендуется предусмотреть индикацию вызова деструктора, отображая соответствующее информационное сообщение в потоке стандартной диагностики stderr. Для форматного вывода диагностических сообщений следует использовать библиотечные функции fputs и fprintf потокового ввода-вывода системы программирования С и С++.
В общедоступную часть объявления производного класса StrNode необходимо включить декларацию компонентных методов которые реализуют виртуальные интерфейсы базового класса BiNode (identify и insert) при поиске по ключу и обеспечивают требуемую функциональную обработку при прохождении узлов бинарного дерева (print и destroy). Кроме них в общедоступной части класса StrNode целесообразно дополнительно декларировать 2 компонентных метода: search и duplicate. Один - для перегрузки наследованного базового компонентного метода search, который реализует универсальный поиск по бинарному дереву. Второй - для индикации результатов поиска. Все перечисленные компонентные методы производного класса StrNode имеют короткий код и могут быть специфицированы как inline-подстановки непосредственно в объявлении класса StrNode.
Компонентный метод identify перегружает соответствующую чистую виртуальную функцию базового класса BiNode, реализуя специфичный для производного класса StrNode способ сравнения ключей при поиске по бинарному дереву. Учитывая символьный тип информационного поля в классе StrNode, рекомендуется применить для сравнения ключей библиотечную функцию strcmp системы программирования С и С++. Аргументами функции strcmp в компонентном методе identify должны быть адрес переданного ключа и адрес из информационного поля текущего узла (str), соответственно. Чтобы соблюсти соответствие типов данных, адрес ключа поиска, переданный как указатель типа (void*), следует явно преобразовать к типу (char*) при подстановке в функцию strcmp. Код возврата функции strcmp рассматривается как код возврата компонентного метода identify и используется как указано в базовом методе search. Компонентный метод insert перегружает соответствующую чистую виртуальную функцию базового класса BiNode для того, чтобы обеспечить создание нового узла бинарного дерева как объекта производного класса StrNode, когда это необходимо в базовом компонентном методе search. Создание нового узла осуществляет конструктор класса StrNode, вызов которого в методе insert должен инициировать оператор new системы программирования С++. Полученный через аргумент адрес необнаруженного ключа поиска (типа void*) следует передавать конструктору производного класса в операторе new после явного преобразования к типу (char*). Явное преобразование типа необходимо, поскольку в производном классе StrNode не определен никакой другой конструктор, кроме StrNode (char*). При успешном завершении в данном контексте оператор new возвратит адрес нового узла бинарного дерева в производном классе StrNode. Этот адрес следует рассматривать как возврат компонентного метода insert. Следующий фрагмент С++ кода можно рассматривать как рекомендуемый вариант спецификации компонентного метода insert:

  class StrNode : public BiNode
  {
  ................................
  BiNode * insert (void * s)
  {
   return (new StrNode ((char*) s));
  }
  ................................
  };

Возврат оператора new в данном контексте будет иметь тип (StrNode*), который автоматически приводится к типу (BiNode*) как требует спецификация метода insert в базовом и производном классе. Указанное преобразование типа является корректным, т. к. система программирования С++ допускает присвоение адреса объекта производного класса по адресу базового класса и выполняет его автоматически, т. е. (StrNode*) может быть использован там, где ожидается (BiNode*). Полученный адрес нового узла в классе StrNode используется соответствующим образом в наследованном от базового класса методе search, как того требует алгоритм поиска по бинарному дереву.
Следует отметить, что неявное преобразование типа при присваивании адреса объекта базового класса указателю на производный класс не считается корректным в системе программирования С++. Поэтому код возврата базового компонентного метода search, имеющий тип (BiNode*),нельзя непосредственно присвоить переменной типа указателя на производный класс (StrNode*), например, в основной функции main программы uni. Для согласования типов указателей в данном случае рекомендуется перегрузка базового метода search в производном классе StrNode, которая может быть специфицирована, например, следующим образом:

  class StrNode : public BiNode
  {
  .............................
  StrNode*search (void*s)
  {
   return ((StrNode*) BiNode::search (s));
  };
  ..............................
  };

Актуальность перегрузки базового компонентного метода search в производном классе StrNode объясняется необходимостью использовать код возврата этого метода для возврата для отображения результатов поиска компонентным методом duplicate, который должен вызываться через объект или указатель на объект производного класса StrNode. Этот метод не должен возвращать значение   или иметь аргументы. Он должен отображать в поток стандартной диагностики (stderr) предупреждение, о том, что при поиске по бинарному дереву обнаружен дубликат ключа. Для отображения предупреждения компонентный метод duplicate может использовать библиотечную функцию fprintf или fputs системы программирования С и С++. При нулевом (NULL) возврате компонентного метода search, когда дубликат ключа не обнаружен, метод dublicate вызываться не должен.
Функциональная обработка узлов при прохождении узлов бинарного дерева в производном классе StrNode должна предусматривать отображение информационного поля str каждого узла и уничтожение узлов. Для выполнения указанной обработки рекомендуется предусмотреть в классе StrNode компонентные методы print и destroy, соответственно. Эти компонентные методы не должны иметь аргументы и код возврата. Их адреса предназначены для передачи в базовые методы прохождения бинарного дерева (preorder, intorder и postorder), и их код очень прост. В частности, компонентный метод print должен только вызвать библиотечную функцию puts системы программирования С и С++ для отображения символьной строки str информационного поля текущего узла бинарного дерева в классе StrNode через поток стандартного вывода (stdout). Предполагая динамическое распределение памяти для хранения узлов бинарного дерева в классе StrNode, компонентный метод destroy должен только использовать оператор delete, чтобы инициировать деструктор класса. Например, спецификация компонентного метода destroy в классе StrNode может иметь следующий формат:

 class StrNode : public BiNode
  {
  .........................
  void destroy() { delete this; return; };
  .........................
  };

Компонентные методы print и destroy могут быть вызваны обычным образом через объекты, ссылки или адреса объектов класса StrNode для индивидуальной обработки узлов бинарного дерева. Кроме того, выбор прототипов этих методов позволяет передавать их адреса наследованным методам preorder, inorder и postorder для выполнения систематической функциональной обработки узлов при прохождении бинарного дерева в прямом, симметричном и концевом порядке, соответственно. Для того, чтобы обеспечить корректность передачи достаточно выполнить явное преобразование их адресов к типу VISIT, декларированному для аргументов базовых методов прохождения бинарных деревьев. Формат преобразования типа демонстрирует следующий пример обращения к наследованному базовому методу inorder для отображения информационных полей узлов бинарного дерева из объектов класса StrNode в симметричном порядке, начиная с корня (root):

  root -> inorder ((VISIT) & StrNode :: print );

Указанное преобразование типа необходимо, потому что специфицированные в базовом классе компонентные методы прохождения бинарного дерева ожидают получить через аргумент указатель на компонентный метод базового класса BiNode, а не указатель на компонентный метод производного класса StrNode. Аналогичный формат следует использовать для обращения, например, к наследованному компонентному методу postorder при прохождении бинарного дерева в концевом порядке с целью очистки памяти его узлов компонентным методом destroy производного класса StrNode. В обоих случаях реализуется механизм косвенной адресации компонентных методов, который позволяет обращаться к компонентам через их адреса в структуре класса.
Перечисленные компонентные методы производного класса StrNode могут быть использованы в основной функции main программы uni по 2-х этапной схеме обработки бинарных деревьев, где этап поиска обеспечивает компонентный метод search (в сочетании с компонентным методом duplicate для индикации обнаруженных дубликатов), а этап прохождения реализуют компонентные методы inorder и postorder, которым передаются адреса компонентных методов print и destroy, чтобы осуществить требуемую функциональную обработку узлов.
Обращение к компонентным методам производного класса StrNode в основной функции main следует осуществлять через указатель на объекты производного класса (StrNode*). Для доступа к динамически распределенным узлам бинарного дерева из объектов производного класса, следует хранить адрес корня, зарезервировав для этой цели отдельную автоматическую переменную (например root) в функции main, типа (StrNode*).

1. Расширить классы бинарных деревьев, чтобы при поиске иметь возможность определять число повторений каждого дубликата.
2. Расширить класс бинарных деревьев для измерения метрических характеристик узлов, определения высоты бинарного дерева, а также общего числа узлов и ветвей в нем.
3. Разработать компонентные методы представления бинарных деревьев в формате вложенных скобок, уступчатого списка и десятичной системе Дьюи.
4. Разработать итерационные программные реализации компонентных методов прохождения бинарных деревьев в прямом, симметричном и концевом порядке.
5. Разработать компонентный метод, который формирует представление бинарного дерева, принятое в теории графов.

1. Д. Райли
   Абстракция и структуры данных. Вводный курс - М.,Мир, 1993
2. Д. Кнут
   Искусство программирования для ЭВМ. Т1, Основные алгоритмы-М., Мир,1976
3. Д. Кнут
   Искусство программирования для ЭВМ. Т3, Сортировка и поиск-М., Мир,1978
4. Э. Рейнголд, Ю. Нивергельт, Н. Део
   Комбинаторные алгоритмы. Теория и практика.- М.,Мир, 1980
5. А. Е. Костин, В. Ф. Шаньгин
   Организация и обработка структур данных в вычислительных системах-М.,Высшая школа, 1987
6. С. Дьюхарст, К. Старк
   Программирование на С++. - Киев НИПФ "ДиаСофт", 1993