Теория механизмов и механика машин

ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЙ

По курсу теории механизмов и механика машин выполняются два домашних задания. Первое посвящается структурному и кинематическому исследованию плоского рычажного механизма, второе – силовому расчету этого же механизма. Задания выполняются графо-аналитически и с использованием стандартных программ на ПЭВМ.

Исходными данными первого задания (см. раздел iv) являются кинематическая схема механизма, а также скорость и ускорение одного из звеньев для конкретного его положения, определяемого углом . Числовые значения длин звеньев и заданных кинематических параметров даны в таблицах исходных данных к заданиям.

Требуется: определить число степеней свободы механизма и число избыточных связей в нем, провести его структурный анализ по Л.В.Ассуру и устранить избыточные связи, выполнить кинематическое исследование его, определив линейные скорости и ускорения точек звеньев, угловые скорости и ускорения звеньев, передаточные функции скоростей точек и звеньев. Кинематическое исследование заданного рычажного механизма рекомендуется выполнить графическим методом – методом планов скоростей и ускорений. Этот метод прост, нагляден и дает возможность быстрого контроля расчетов, выполненных на ЭВМ. Поэтому такой метод имеет широкое распространение в инженерной практике. Базируется этот метод на графическом решении векторных уравнений, связывающих скорости и ускорения отдельных точек звеньев механизма. Эти уравнения составляются на основе теорем о плоском движении тела и сложном движении точки.

Порядок выполнения первого задания:

Строят схему механизма по заданным размерам методом засечек в положении, определяемом углом начального звена, в масштабе. Значение масштаба рассчитывают по формуле:

Масштаб длин будет (в миллиметрах на метр); масштаб плана скоростей (в миллиметрах на метр-секунду в минус первой степени), масштаб плана ускорений (в миллиметрах на метр-секунду в минус второй степени)

Длина отрезка (в миллиметрах), изображающая на схеме начальное звено, берется произвольно. Но целесообразно брать ее кратной реальной длине звена. Размеры остальных звеньев находятся с учетом выбранного масштаба длин. Последовательность построения схемы механизма дана в разделах i и ii.
Определяют число степеней свободы механизма по формуле П.Л.Чебышева для плоских механизмов (без избыточных связей)
;

здесь – число всех звеньев, включая стойку; – число подвижных звеньев; – число низших одноподвижных (вращательных и поступательных) кинематических пар; – число высших двухподвижных кинематических пар (в рычажных механизмах их нет). Полученное число степеней свободы механизма соответствует числу начальных звеньев с заданными кинематическими параметрами, так как только в этом случае остальные звенья будут двигаться вполне определенным образом относительно стойки. Число избыточных связей в механизме находят (по формуле А.П.Малышева)

где , , – число трех-, четырех-, пятиподвижных кинематических пар.

При изучении характера движения звеньев и вида кинематических пар особое внимание следует обратить на сложное движение: сочетание относительного поступательного с переносным вращательным.
Проводят структурный анализ механизма по Л.В.Ассуру, согласно теории которого любой плоский механизм с состоит из первичного механизма (одноподвижное начальное звено и стойка, образующие вращательную или поступательную кинематическую пару) с заданным законом движения начального звена () и одной или нескольких структурных групп (незамкнутая кинематическая цепь, которая при замыкании со стойкой обращается в неподвижное соединение и у которой ). В заданиях (см. раздел iv) встречаются, как правило, двухповодковые группы, состоящие из двух звеньев и трех кинематических пар.

Структурный анализ начинают с установления первичного механизма, закон движения которого задан. Затем выделяют ту структурную группу, которая была присоединена к механизму последней, и далее – оставшуюся структурную группу, примыкающую к первичному механизму (для механизмов, имеющих по две структурные группы). Расчленение механизма на структурные группы производят так, чтобы после удаления группы из механизма не нарушался закон движения оставшихся звеньев механизма и число его степеней свободы. Для каждой структурной группы по формуле А.П.Малышева находят число избыточных связей, устраняют их увеличением подвижностей кинематических пар, и составляют схему самоустанавливающегося механизма.

Строят планы линейных скоростей и ускорений точек звеньев и определяют угловые скорости и ускорения звеньев.
Построение планов скоростей начинают со звена, закон движения которого задан. Определяют скорость точки этого звена, составляют векторное уравнение, связывающее эту скорость со скоростями точек смежного звена, и устанавливают какие векторы известны по величине, какие и по величине, и по направлению или какие только по направлению. Рекомендуется векторы, известные по величине и по направлению, подчеркивать двумя чертами, а известные только по величине или только по направлению – одной чертой. Здесь же отмечают буквами направление векторов. Если в векторном уравнении только два неизвестных, то оно решается, и его графическим решением будет план скоростей. Стрелки векторов на плане проставляют в строгом соответствии с записанным уравнением, соблюдая правило векторного суммирования; при этом относительные скорости проходят вне полюса, а начала векторов абсолютных скоростей всегда находятся в полюсе. Из построенного плана находят отрезки, пропорциональные скоростям точек, и, зная масштаб , определяют скорости, а направление скоростей - из плана.

Если известны абсолютные скорости двух точек одного и того же звена, то скорость третьей точки, лежащей с ними на одной прямой, находят пропорциональным делением (например, точка s₂). Для этого на плане скоростей отрезок относительной скорости делят искомой точкой в том же соотношении, в котором соответствующая точка делит реальное звено на схеме механизма. Длину искомого отрезка определяют из пропорции (отношение длин на звене механизма равно отношению отрезков на плане скоростей). Соединяя полученную точку с полюсом, находят отрезок искомой абсолютной скорости.

Абсолютную скорость третьей точки звена, не лежащей на одной прямой с двумя другими его точками, скорости которых известны, определяют методом подобия. Для этого на плане скоростей на отрезке известной относительной скорости строят треугольник, подобный тому, который имеется на схеме механизма, соблюдая одинаковое направление прочтения букв по вершинам треугольника на плане скоростей и на механизме. При этом стороны подобных треугольников взаимно перпендикулярны. В итоге построения получается треугольник, составленный вершинами относительных скоростей. Соединяя построенную вершину треугольника с полюсом, находят отрезок искомой абсолютной скорости.

Если два звена образуют поступательную кинематическую пару, то для определения абсолютной скорости точки одного из этих звеньев, геометрически совпадающей в данный момент с точкой другого звена (скорость которой известна), используют векторное уравнение сложного движения. Абсолютная скорость искомой точки складывается из переносной и относительной составляющих; вектор переносной скорости обычно известен.

Зная линейные скорости точек, определяют угловые скорости звеньев по величине и по направлению.

План ускорений строят на основе векторных уравнений в той же последовательности, что и план скоростей. Каждый из векторов представляют нормальной и касательной составляющими. При этом нормальное ускорение всегда известно по величине (так как план скоростей построен) и направлению (к центру вращения), а касательное перпендикулярно ему и неизвестно по величине. В этих уравнениях также дважды подчеркивают снизу векторы, известные по величине и по направлению. Так, для вектора , направленного от точки С к точке В (центр относительного вращения), внизу пишут С® В.

На плане ускорений начало вектора абсолютного ускорения всегда находится в полюсе, а вектор относительного ускорения проходит вне полюса.

Метод пропорционального деления и метод подобия применяют только для полных относительных ускорений. При этом подобную фигуру следует строить на плане по трем сторонам, величина одной из которых известна, а две другие определяют из соответствующих пропорций, соблюдая одинаковое направление обхода при чтении букв по вершинам фигуры, составленной из полных относительных ускорений плана, и фигуры на звене механизма.

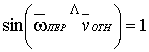Полное ускорение точки, совершающей сложное движение, состоит из переносного, относительного и кориолисового ускорений. Последнее обусловлено тем, что звенья, имеющие линейную относительную скорость , совершают вращательное движение с угловой скоростью вокруг мгновенного центра вращения. Для плоского механизма , так как в этом случае . Направление находят по правилу Жуковского поворотом вектора на 90° в направлении угловой скорости . Определив из плана касательные ускорения, подсчитывают величины угловых ускорений e звеньев и определяют их направления.

Кинематические передаточные функции скоростей точек и звеньев механизма (первая производная от функции положения по ) являются характеристиками только геометрии самого механизма и не зависят от скорости начального звена. Это позволяет использовать их для оценки кинематических возможностей механизма при изучении его динамики. Величины передаточных функций скоростей могут быть определены через отрезки плана скоростей и длины звеньев. Например, или , где - передаточное отношение (передаточная функция угловой скорости).

Исходными данными второго задания (см. раздел iv) являются: кинематическая схема механизма (та же, что и в первом), линейные ускорения центров масс звеньев и угловые ускорения звеньев; массы звеньев и их моменты инерции относительно осей, проходящих через центры масс, внешние силы. Числовые значения этих параметров приведены в исходных данных к заданиям, а величины ускорений определены при выполнении первого задания.

Требуется определить: реакции (силы) в кинематических парах (без учета трения) и неизвестный внешний силовой фактор (момент или силу).

Эти силы необходимо знать для выполнения расчетов на прочность, жесткость, виброустойчивость, а также для оценки необходимой мощности двигателя.

Порядок расчета второго задания:

Определяют силы на основе метода кинетостатики, согласно которому к действующим на звено (группу звеньев или на механизм) реальным силам и моментам сил добавляются расчетные (главный вектор сил инерции и главный момент сил инерции ), и рассматривают мгновенное равновесное состояние звена. При этом составляют векторное уравнение сил и уравнение моментов сил и находят искомые величины. По векторному уравнению сил в масштабе (в миллиметрах на ньютон) строят план сил, который избавляет от необходимости брать проекции сил на координатные оси и составлять два уравнения проекций сил на оси. Метод планов сил значительно ускоряет решение и позволяет быстро оценивать результаты, получаемые с помощью ЭВМ. Поэтому такой метод широко распространен в инженерной практике.
Силовой расчет начинают с той структурной группы, которая была присоединена к механизму последней (как правило, к одному из ее звеньев приложены известные внешние силы или внешние моменты). Для каждой структурной группы составляют векторные уравнения сил, строят планы сил и определяют искомые силы. Если число неизвестных в векторном уравнении сил больше двух, то записывают еще и уравнение моментов. Затем проводят силовой расчет отдельных звеньев, входящих в данную структурную группу. Используя найденные значения сил, переходят к следующей группе. В последнюю очередь определяют неизвестный силовой фактор. В уравнениях сил также следует отмечать двумя чертами внизу силы, известные и по величине, и по направлению, одной чертой – силы, известные либо только по величине, либо только по направлению.

Силовой расчет двухповодковых структурных групп рекомендуется выполнять в такой последовательности:

Если структурная группа состоит из двух звеньев, соединенных вращательной кинематической парой и имеющих свободные элементы двух поступательных кинематических пар (например, группа из звеньев 4 и 5 в исходных данных к заданиям 3, 5 или группа из звеньев 4 и 5 в задании 26, см. раздел iv), то силы в поступательных кинематических парах определяют из векторного уравнения сил для структурной группы, а точки приложения этих сил из уравнения моментов относительно оси общего шарнира для каждого из звеньев.
Если структурная группа состоит из двух звеньев, соединенных вращательной кинематической парой и имеющих свободные элементы двух вращательных кинематических пар (например, группа из звеньев 2 и 3 в исходных данных к заданиям 7 и 8, см. раздел iv), то внешние неизвестные силы в вращательных кинематических парах представляют в виде двух составляющих: нормальной (вдоль звена) и касательной (перпендикулярно звену). Касательные составляющие находят из уравнений моментов сил для каждого из звеньев относительно оси центрального (общего) шарнира, а нормальные составляющие – из векторного уравнения сил для каждой структурной группы.
Если структурная группа состоит из двух звеньев, соединенных вращательной кинематической парой и одно из которых имеет свободный элемент поступательной кинематической пары, а другое – свободный элемент вращательной кинематической пары (например, группа из звеньев 4 и 5 в исходных данных к заданию 15, см. раздел iv), то силу во внешней вращательной кинематической паре представляют в виде двух составляющих: нормальной (вдоль звена) и касательной (перпендикулярно звену). Касательную составляющую находят из уравнения моментов сил для этого из звена относительно оси центрального (общего) шарнира, а нормальную составляющую и силу в поступательной кинематической паре – из векторного уравнения сил для всей структурной группы. При силовом расчете рассмотренных структурных групп силу в центральном шарнире определяют из векторного уравнения сил для отдельного звена.
Если структурная группа состоит из двух звеньев, соединенных поступательной кинематической парой и имеющих свободные элементы вращательных кинематических пар (например, группа из звеньев 2 и 3 в исходных данных к заданию 11, см. раздел iv), то внешнюю силу в шарнире одного из звеньев (например, шарнир В в задании 11, см. раздел iv), направленную (если сила тяжести звена мала) перпендикулярно другому звену группы, определяют из уравнений моментов сил для структурной группы относительно оси (точка С) второго шарнира. Силу во втором шарнире, неизвестную ни по величине, ни по направлению, находят из векторного уравнения сил для структурной группы, а силу в поступательной кинематической паре – из векторного уравнения сил для любого из звеньев.

Векторные уравнения для определения скоростей, ускорений, сил записываются на основных листах, а результаты вычислений заносятся в таблицы (см. рисунки и таблицы разделов i и i i ). Все пояснения к построениям и расчеты выполняют в расчетно-пояснительной записке.

Для расчета на ЭВМ рекомендуется использовать один из диалоговых программных комплексов (diada, САРЦМ, БЛОМСАР).

Ввод исходных данных в каждом из них осуществляется в диалоге. ЭВМ рассчитывает кинематические передаточные функции элементов механизма для ряда его последовательных положений, траекторий точек, связанных со звеньями, определяет реакции в кинематических парах.