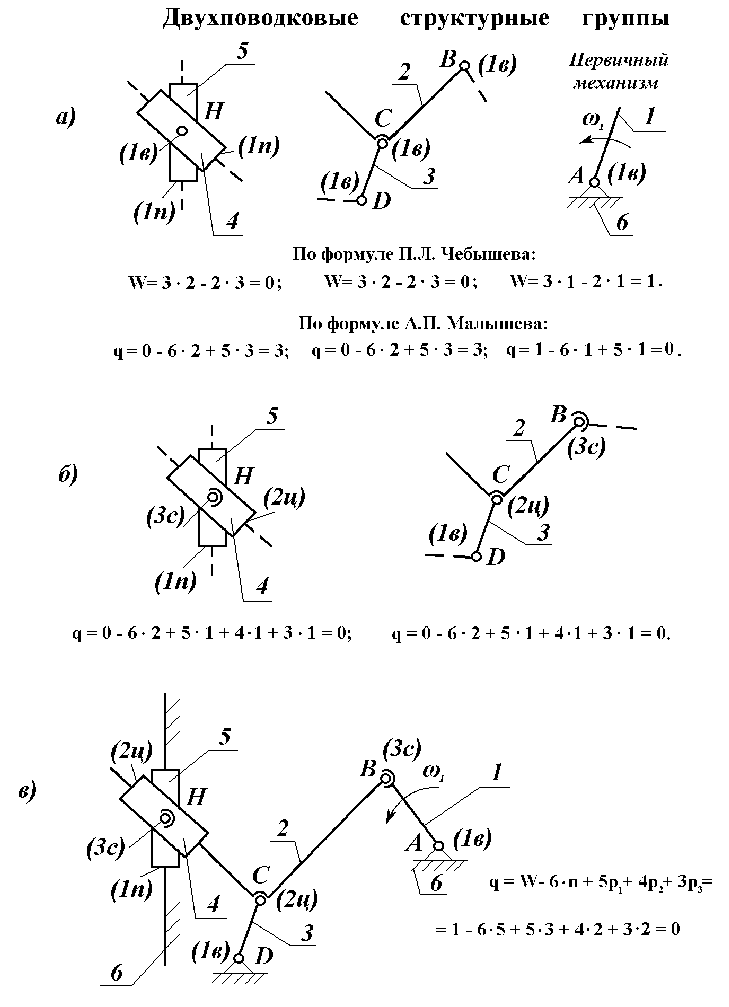
Рис.1.2.
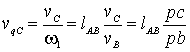 , м;
, м; 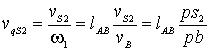 , м;
, м; 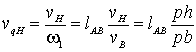 , м;
, м; 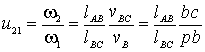 ;
;
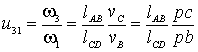 .
.
![]() . (1.4)
. (1.4)
Нормальное ускорение подсчитывают по формуле ![]() = = 22/0,1 = 40 м/с2, касательное – по формуле
= = 22/0,1 = 40 м/с2, касательное – по формуле ![]() = 80*0,1 м/с2. Уравнение для определения ускорения точки c звена 2 имеет вид
= 80*0,1 м/с2. Уравнение для определения ускорения точки c звена 2 имеет вид
![]() . (1.5)
. (1.5)
Каждый вектор уравнения (1.5) представляют в виде нормальной и касательной составляющих:
![]() . (1.5')
. (1.5')
Для каждого вектора нормального ускорения отмечают конкретное направление по отношению к точкам звеньев механизма (b® a и т. д.).
Нормальные ускорения находятся по формулам
![]() = 2,342/0,15 = 36,2 м/с2;
= 2,342/0,15 = 36,2 м/с2; ![]() = 2,34/0,3 = =18,1 м/с2. Выбрав отрезок
= 2,34/0,3 = =18,1 м/с2. Выбрав отрезок ![]() =80 мм, вычисляют масштаб плана ускорений
=80 мм, вычисляют масштаб плана ускорений ![]() = 80/40 = 2 мм/м? с-2. Для построения плана ускорений (см. рис.1.1 г) из полюса p' проводят прямую, параллельную звену 1 (ab), и на ней откладывают отрезок
= 80/40 = 2 мм/м? с-2. Для построения плана ускорений (см. рис.1.1 г) из полюса p' проводят прямую, параллельную звену 1 (ab), и на ней откладывают отрезок ![]() = 40* 2 = 80 мм, направление которого соответствует направлению вектора
= 40* 2 = 80 мм, направление которого соответствует направлению вектора ![]() , т.е. от точки b к центру вращения (точке a). Из точки
, т.е. от точки b к центру вращения (точке a). Из точки ![]() откладывают перпендикулярно к ab отрезок
откладывают перпендикулярно к ab отрезок ![]() = 8? 2 = 16 мм, учитывая направление
= 8? 2 = 16 мм, учитывая направление ![]() . Соединив на плане точку b' с p', получают отрезок, пропорциональный полному ускорению точки b,
. Соединив на плане точку b' с p', получают отрезок, пропорциональный полному ускорению точки b, ![]() = 81/2 = 40,5 м/с2.
= 81/2 = 40,5 м/с2.
Из точки проводят прямую, параллельную стержню bc, и откладывают на ней отрезок нормального относительного ускорения ![]() = 18,1* 2 = 36,2 мм так, чтобы он был направлен от точки c к точке b механизма. Так как для вектора касательного относительного ускорения
= 18,1* 2 = 36,2 мм так, чтобы он был направлен от точки c к точке b механизма. Так как для вектора касательного относительного ускорения ![]() известно только направление линии его действия (
известно только направление линии его действия (![]() ^ bc), то проводят прямую из точки
^ bc), то проводят прямую из точки ![]() , перпендикулярную стержню bc. Векторы левой части уравнения (1.5') начинают строить из полюса p'. Сначала проводят прямую, параллельную звену 3 (стержню cd), и на ней откладывают отрезок
, перпендикулярную стержню bc. Векторы левой части уравнения (1.5') начинают строить из полюса p'. Сначала проводят прямую, параллельную звену 3 (стержню cd), и на ней откладывают отрезок ![]() = 36,2*2 = 72,4 мм в направлении от тоски c к центру вращения (точка d). Для нахождения вектора касательного ускорения
= 36,2*2 = 72,4 мм в направлении от тоски c к центру вращения (точка d). Для нахождения вектора касательного ускорения ![]() из точки
из точки ![]() проводят прямую, перпендикулярную стержню cd, до пересечения в точке c с прямой, проведенной из точки
проводят прямую, перпендикулярную стержню cd, до пересечения в точке c с прямой, проведенной из точки ![]() перпендикулярно стержню bc. Соединив точки p' и c' , получают отрезок p'c', пропорциональный полному ускорению точки c. Значение этого ускорения
перпендикулярно стержню bc. Соединив точки p' и c' , получают отрезок p'c', пропорциональный полному ускорению точки c. Значение этого ускорения ![]() = 149/2 = 74,5 м/с2. На построенном плане ускорений проставляют стрелки, показывающие, согласно уравнению (1.5'), направления ускорений
= 149/2 = 74,5 м/с2. На построенном плане ускорений проставляют стрелки, показывающие, согласно уравнению (1.5'), направления ускорений ![]() и
и ![]() , находят значения этих ускорений:
, находят значения этих ускорений: ![]() = 60/2 = 30 м/с2,
= 60/2 = 30 м/с2, ![]() = 131/2 = 65,5 м/с2.
= 131/2 = 65,5 м/с2.
Соединив точки b' и c' на плане, получают отрезок b'c', пропорциональный ![]() - полному относительному ускорению. Тогда
- полному относительному ускорению. Тогда ![]() = 70/2 = 35 м/с2.
= 70/2 = 35 м/с2.
Ускорение ![]() точки s2 звена 2 определяют способом пропорционального деления. Для этого отрезок b'c' делят точкой
точки s2 звена 2 определяют способом пропорционального деления. Для этого отрезок b'c' делят точкой ![]() в отношении
в отношении ![]() . Тогда
. Тогда
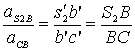 ;
; ![]() = 47,0 мм.
= 47,0 мм.
От точки b' на прямой b'c' откладывают отрезок ![]() и соединяют p' с точкой
и соединяют p' с точкой ![]() . Полученный отрезок
. Полученный отрезок ![]() пропорционален полному ускорению
пропорционален полному ускорению ![]() = 126,4/2 = 63,2 м/с2.
= 126,4/2 = 63,2 м/с2.
Чтобы найти ускорение точки h4,5, используют теорему о сложении ускорений при сложном движении, когда переносное движение не поступательное. Записывают
![]() или
или ![]() , (1.6)
, (1.6)
где ![]() - ускорение а переносном движении (полное ускорение точки l2 звена 2);
- ускорение а переносном движении (полное ускорение точки l2 звена 2);
![]() - ускорение в относительном поступательном движении втулки 4 по стержню cl;
- ускорение в относительном поступательном движении втулки 4 по стержню cl;
![]() - кориолисово (поворотное) ускорение.
- кориолисово (поворотное) ускорение.
Ускорение ![]() точки l2 звена 2 определяют, как и ее скорость, методом подобия. Для этого на отрезке b'c' плана ускорений строят d b'c'l' (заштрихован на рис. 1.1 г), подобный d bcl на звене 2. Так как ? bcl = 90° , то на плане проводят через точку c' прямую, перпендикулярную отрезку b'c', и откладывают на ней отрезок b'l', найденный из соотношения
точки l2 звена 2 определяют, как и ее скорость, методом подобия. Для этого на отрезке b'c' плана ускорений строят d b'c'l' (заштрихован на рис. 1.1 г), подобный d bcl на звене 2. Так как ? bcl = 90° , то на плане проводят через точку c' прямую, перпендикулярную отрезку b'c', и откладывают на ней отрезок b'l', найденный из соотношения ![]() ,
, ![]() = 35,5 мм.
= 35,5 мм.
Положение точки l' находят по правилу обхода вершин. Обход вершин d bcl на звене 2 по часовой стрелке осуществляют от точки b к точке c, от точки c к точке l. Тот же порядок чередования вершин сохраняется и на плане ускорений: b'® c'® l'. Соединяя точки b' и l' , получают d b'c'l' подобный d bcl. Полюс плана p' соединяют с точкой l' и получают отрезок p' l', пропорциональный искомому вектору полного ускорения ![]() точки l2 звена 2. Значение
точки l2 звена 2. Значение ![]() = 158/2 = 79 м/с2.
= 158/2 = 79 м/с2.
Представляя векторы ускорений в уравнении (1.6) в виде составляющих, получают
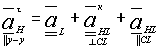 . (1.6')
. (1.6')
Нормальная составляющая относительного ускорения ![]() , так как движение втулки 4 относительно стержня cl прямолинейное (r =
, так как движение втулки 4 относительно стержня cl прямолинейное (r =![]() ). Значение ускорения
). Значение ускорения ![]() подсчитывается по формуле
подсчитывается по формуле
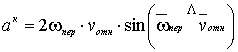 .
.
Переносное движение осуществляет звено 2. Поэтому ![]() - угловая скорость звена 2. Так как для плоского механизма
- угловая скорость звена 2. Так как для плоского механизма 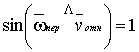 , то окончательно формула для определения кориолисова ускорения
, то окончательно формула для определения кориолисова ускорения ![]() имеет вид
имеет вид ![]() . Значение
. Значение ![]() = 40,3 м/с2. Направление кориолисова ускорения
= 40,3 м/с2. Направление кориолисова ускорения ![]() находят по правилу Жуковского поворотом вектора
находят по правилу Жуковского поворотом вектора ![]() относительной скорости на 90° в сторону угловой скорости
относительной скорости на 90° в сторону угловой скорости ![]() переносного движения (см. рис.1.1 д). Для графического решения уравнения (1.6') на плане ускорений из точки l' проводят прямую, параллельную вектору
переносного движения (см. рис.1.1 д). Для графического решения уравнения (1.6') на плане ускорений из точки l' проводят прямую, параллельную вектору ![]() (см. рис.1.1 д), и откладывают на ней отрезок
(см. рис.1.1 д), и откладывают на ней отрезок ![]() = 40,3* 2 = 80,6 мм. Через точку khl проводят прямую, параллельную стержню cl (линии действия относительного касательного ускорения
= 40,3* 2 = 80,6 мм. Через точку khl проводят прямую, параллельную стержню cl (линии действия относительного касательного ускорения ![]() ); величина вектора
); величина вектора ![]() неизвестна. Из полюса p' проводят прямую, параллельную направляющей y-y, по которой перемещается ползун 5. Пересечение этой прямой в точке h' с прямой, проведенной через точку khl параллельно стержню cl, дает решение векторного уравнения (1.6'). Полученные отрезки p'h' и khll' соответственно пропорциональны ускорениям
неизвестна. Из полюса p' проводят прямую, параллельную направляющей y-y, по которой перемещается ползун 5. Пересечение этой прямой в точке h' с прямой, проведенной через точку khl параллельно стержню cl, дает решение векторного уравнения (1.6'). Полученные отрезки p'h' и khll' соответственно пропорциональны ускорениям ![]() и
и ![]() . Тогда
. Тогда ![]() = 90/2 = 45 м/с2,
= 90/2 = 45 м/с2, ![]() = 82/2 = 41 м/с2. Звено 5 движется поступательно, поэтому ускорение его центра масс
= 82/2 = 41 м/с2. Звено 5 движется поступательно, поэтому ускорение его центра масс ![]() = 45 м/с2.
= 45 м/с2.
Определение угловых ускорений звеньев 2 и 3: ![]() = 30/0,3 = 100 рад* с-2;
= 30/0,3 = 100 рад* с-2; ![]() = 65,5/0,15 = 435 рад* с-2.
= 65,5/0,15 = 435 рад* с-2.
Направления угловых ускорений находят подобно тому, как были найдены направления угловых скоростей (см. рис.1.1 е, ж), и отмечают эти направления круговыми стрелками в табл. 1.1.